诞生 100 年，这个简单的物理模型难倒了无数物理学家

科学无国界

我们是知识的搬运工

认真阅读下面的文章，并思考文末互动提出的问题，严格按照 互动：你的答案格式在评论区留言，就有机会获得由湛庐文化/四川人民出版社提供的优质科普书籍《宇宙的最后三分钟》一本。

“

从磁体，到大脑——伊辛模型诞生一百年后，解释了万事万物。

”

Samuel Velasco/Quanta Magazine

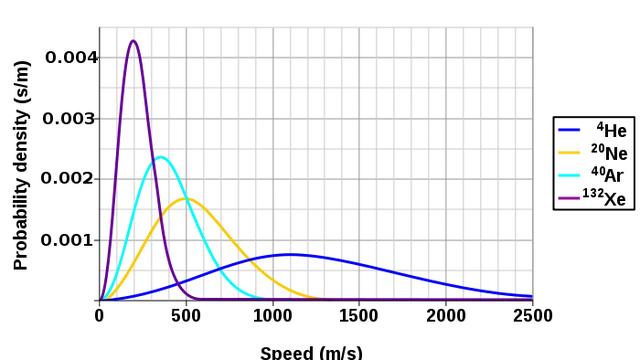
在伊辛模型中，热运动使箭头随机翻转，而磁的吸引让相邻箭头方向一致，这两种力量相互竞争，决定着物质的这些微观特性。真实世界中的许多系统中，也存在着同样的竞争。

水结成冰，汤被煮沸……这种突然而彻底的物态转变，在20世纪之前对人们来说还是神秘的。科学家观察到，物质常常是逐渐变化的：将一堆原子微微加热，体积会微微膨胀。但是如果在材料的临界点附近轻轻推动一下，它就会变成与之前完全不同的东西。

破解“相变”谜题的数学关键在 100 年前首次被发现，并改变了整个自然科学的面貌。众所周知，伊辛模型最初提出时是关于磁体的漫画式理论；现在则作为物理系统的简单模型被广泛使用——伊辛模型之于物理学家，就像果蝇之于生物学家。最近出版的一本教科书认为，伊辛模型“可以对几乎所有有趣的热力学现象建模”。

它甚至渗透进与物理学关系很远的学科，成为研究地震、蛋白质、大脑甚至种族隔离的模型。

一个研究磁性的简化模型，究竟如何简明地解释了相变，如何在科学中遍地开花，又是如何在今天继续推动着知识边界的扩张？且听我为您娓娓道来。

1920年，世界正从一场全球性的流感中恢复元气。一位名叫威廉·楞次的德国物理学家，开始研究为什么磁体被加热到某个温度以上就会突然失去吸引力，这一现象是皮埃尔·居里在25年前发现的。楞次把磁体想象成排列成格子的小箭头，每个箭头代表了一个原子，要么指向上，要么指向下。（原子本质上具有磁性，有南北极，因此可以确定每个原子的方向。）邻近的箭头会相互影响，一个箭头会试图翻转旁边磁性相反的箭头，好让它们与自己方向一致。

楞次注意到，如果大多数原子指向相同，每个原子的微小磁场凝聚起来，就会让材料整体表现出磁性。但如果相同数量的“上”原子和“下”原子均匀混合在一起，它们就相互抵消，不会显现出很强的磁性。

单单是关于晶体格子之间热与磁的竞争的研究，就发表了数以千计的物理论文。热（粒子的随机颤动）为无序而战；而磁致力于抵抗这种无序。楞次认为，在温度很低的时候，磁性所维持的秩序获胜。然而有足够多的热量时，原子之间的随机推挤就会打破它们之间的稳定关系，这就解释了居里观察到的磁体在高温时丧失“魔力”的现象。

楞次责成他的研究生恩斯特·伊辛（Ernst Ising）研究细节。虽然真正的磁体是三维的，但伊辛将情况简化为一个线性的箭头链，链上的每个箭头都受到相邻两个箭头的影响。运用一个现在已经成为大学教科书内容的计算方法，他证明了这条链不能有稳定的磁性，这个模型现在被称为一维伊辛模型。随机翻转在任何温度下都会破坏磁性的一致。加拿大麦克马斯特大学退休教授、凝聚态物理学家约翰·贝林斯基说：“一维只是没有它所需要的东西。”

一维伊辛模型

1925年，伊辛发表了他的研究结果。他和楞次认为这一结果不仅适用于箭头组成的二维薄片，也适用于三维块体，从而这个模型无法描述真实磁体的行为。从这个结果来看，它似乎毋庸置疑地要被丢弃到错误理论的火葬场中去。

尽管如此，因为有人想要探究它在数学上的性质，伊辛模型还是活了下来。在20世纪40年代，这个理论引起了拉斯·昂萨格（Lars Onsager）的兴趣。昂萨格是一位理论物理学家，也是诺贝尔奖得主。他想解出伊辛模型，即在二维情况下算出在任何给定温度下可能指向“上”的原子的比例。对于二维方格子情况，每个箭头都有四个邻近的箭头，而非两个。

解决任何一种情况都需要列一张表格，列出每个箭头对其他箭头的影响。在一个平面上，这些寻找相互作用的问题比在一条线上的复杂得多。计算机科学家索林·伊斯特拉尔（Sorin Istrail）认为，昂萨格在1944年发表的解决方案是一项“非人道”的数学工作，这项工作在很大程度上是难以理解的。伊斯特拉尔说：“一行一行读下去，你只能了解到这个理论是正确的，其余毫无收获。”

昂萨格证明了在二维情况下，事情正如楞次所料：低温时，磁性掌握一切，箭头排列成行；一旦温度超过“临界值”，无序就控制了全局。相变可以用一个简单的相互连接的箭头网格来解释，而不需要像许多物理学家所认为的那样，需要结合真实粒子的混乱性来考虑。

尽管如此，该模型仍在角落中积累灰尘。它似乎过于简化了，像是仿照现实画的一幅超简化的简笔画。“大家觉得这个理论看起来可疑得很。”丹麦罗斯基德大学物理学历史学家马丁·尼斯说。

转机发生了。科学家们测量了氩和氦的性质，过程是困难重重的，结果表明，昂萨格的解与这些物质的“临界指数”完美吻合。这些指数是1/8或7/4这样的数字，它描述了在发生相变前的阶段，各种性质（如热容）的变化速度。尼斯说，到1965年，大多数物理学家都开始重视起楞次和伊辛的箭头，尽管他们还是想知道，为何一个在物理上如此不切实际的图像，能够准确得出物质性质的细节信息。

答案不在于模型，而在于自然。

伊辛模型之所以强大，是因为一系列不相关的物质在发生转变时，都有着相同的临界指数——这一现象现在被称为普适性（universality）。

1971年，美国物理学家肯·威尔逊（Ken Wilson）提出了普适性数学，并为此获得了诺贝尔奖。威尔逊指出，在高温下箭头方向是随机的，当系统冷却接近相变点时，相邻箭头之间的磁吸引力会形成箭头有序排列的“岛”，这些岛会越变越大。临界指数描述了这个过程的细节，比如最大的岛是如何逐渐变大的。

当伊辛模型处于其临界温度时，它包含大大小小由对齐箭头组成的“岛”。|

 

mattbierbaum.github.io

在临界温度下，从一个“小点”到一片“陆地”，各种大小的“岛”同时存在。在这种情况下，即使是两个相距很遥远的箭头，其中一个翻转也会引起另一个翻转，尽管它们并不相邻——这表明系统的宏观属性已经脱离了微观细节。这种对微观细节的超脱就是普适性的魔力。所有具有相同维数和相同对称性的系统都会经历完全相同的相变，无论微观上是铁原子、水分子还是小箭头。

设想一个系统，它包含许多具有相互作用的实体，这些实体可以用相反的标签来描述，例如“上”和“下”，“出席”和“缺席”。普适性意味着，当研究人员想要理解这样的系统时，他们可能会从伊辛模型着手。加州大学伯克利分校的凝聚态物理学家弗朗西斯·赫尔曼（Frances Hellman ）说：“某种程度上，伊辛模型是一种最简单的可解模型。它能帮你在很大程度上理解一件事。”比如说，研究人员可以通过让箭头在一个平面上自由旋转来扩展模型，以适用于其他物理系统。

但是，即使伊辛模型改变了物理学家对材料的理解，研究人员在精确求解三维版本时也遇到了困难——也就是说，要找到一个简洁的公式，来描述任何给定温度下三维箭头晶格的磁化程度。甚至理查德·费曼在试图解决伊辛1920年的原始任务时，也失败了。

现在的计算机可以模拟三维伊辛模型，并将其临界指数近似到一个合理的精度，因此物理学家们并不着急去找一个精确的解决方案，虽然这仍然是人们渴望的事情。2012年，物理学家进行了一项合作，他们宣布，在探索逻辑上可能的物理理论的空间时，找到了一个包含三维伊辛模型精确临界指数的区域。从那时起，该组织进一步缩小了该区域。去年12月，他们应用他们的方法解释了1992年航天飞机飞行过程中一次令人费解的液氦测量。

法国高级科学研究所的物理学家斯拉瓦·里奇科夫（Slava Rychkov）参与了这项工作。他说，费力多算几位小数其实不是重点。在可能的物理理论地图上的其他地方，有伊辛理论的扩展，有奇异粒子的比扎罗宇宙理论，甚至可能还有真实宇宙中难以捉摸的量子引力理论。伊辛模型代表了这个抽象的“理论空间”中最简单的部分之一，因此成为开发探索未知领域的新工具的试验场。

如果它的临界指数可以精确确定，“这个解决途径一定是目前完全未知且全新的”，里奇科夫说，“这也必将带来一场新的革命。”

作者：Charlie Wood

翻译：xux

审校：Nuor

原文链接：

https://www.quantamagazine.org/the-cartoon-picture-of-magnets-that-has-transformed-science-20200624/

tian

福

tian

利

xiang

时

shang

间

今天我们将送出由湛庐文化/四川人民出版社提供的优质科普书籍《宇宙的最后三分钟》。

你想过世界末日的场景吗？宇宙将会在怎样的场景下走向末日？是遭遇小行星撞击，还是遭遇彗星撞击，又或是银河系遭遇另一个星系的撞击？在《宇宙的最后三分钟》，保罗·戴维斯将为你介绍关于宇宙未来的最新理论，带你破解宇宙终结之谜。一本人人读得懂的宇宙学科普著作。

所有你关心的宇宙未来的话题：小行星撞击、热力学第二定律、宇宙诞生的最初三分钟、恒星的末日、黑洞、引力辐射、太空移民、外星智慧生命、循环宇宙模型……你都可以在本书中找到！

【互动问题：如果让你从日常现象中抽象出模型，你能得出哪些模型？】

请大家严格按照互动：问题答案的格式在评论区留言参与互动，格式不符合要求者无效。

*本活动仅限于微信平台

编辑：aki