旅行商问题 (TSP 问题) 是一个 NP-hard 问题,给定若干个城市,求旅行商从某个城市开始,遍历所有城市最终回到出发点的最短路径 (每个城市只经过一次)。求 TSP 的最优解时间较长,本文介绍一种用 SOM 算法求 TSP 近似解的方法,SOM 是竞争神经网络,也称为自组织映射。
1.前言
最近突然翻到读大学时一个小作业的代码,主要用 SOM 网络算法求 TSP 问题近似解。代码参考了论文《A simple learning algorithm for growing ring SOM and its application to TSP》,论文作者用了一种 RSOM 算法,与 SOM 不同,其初始神经元比较少,但是会在训练的过程中不断的增加新的神经元。
代码是用 matlab 编写的,地址:https://github.com/cc54294/SOM_TSP
代码的效果如下面的 gif 所示,分别是在 48、101、225、561 个城市上计算 TSP 的结果。在 48、101、225 个城市上的效果都比较好,但是在 561 个城市上的效果比较差。

48 个城市 TSP 问题

101 个城市 TSP 问题

225 个城市 TSP 问题

561 个城市 TSP 问题
2.TSP 问题
TSP 问题称为旅行商问题,问题的定义:有一个旅行商需要访问 N 个城市,旅行商从一个城市出发,需要经过所有的 N 个城市且每个城市只经过一次,最后回到出发点,求最短的路径。如下图所示,从城市 A 出发,左侧为 TSP 问题的最短路径:

TSP 问题
之前介绍过 Pointer Network,可用于求解 TSP 问题,不熟悉的童鞋可以参考一下之前的文章《指针网络 Pointer Network》。本文介绍另一种神经网络 SOM 用于求解 TSP。
3.SOM 算法
SOM 神经网络 (自组织映射 Self-Organizing Map),是一种竞争型神经网络,通常用于无监督学习。一般的神经网络通过损失函数计算梯度进行优化,而 SOM 采用了竞争的策略。
对于每一个输入样本 x,SOM 会计算所有神经元与 x 的距离 (例如欧式距离),选出获胜神经元 (也称为激活神经元,距离最近的),然后优化获胜神经元附近的网络拓扑结构。常见 SOM 结构如下,包括输入层和输出层 (竞争层):

SOM 示意图
上面的图中,输入层的维度是 d (即每一个样本 x 维度是 d),上面的二维网格中每一个圆点均是一个神经元,每个神经元都具有一个特征向量 w (维度也是 d)。
神经元之间是具有拓扑结构的,常见的拓扑结构有矩形 (Rectangular) 和六边形 (Hexagonal) 的,如下:

SOM 神经元常见的拓扑结构
SOM 训练的过程如下:
- 随机初始化输出层神经元的特征向量 w,维度是 d。
- 对于每一个输入样本 x,找出与其最匹配的神经元,可以根据欧氏距离匹配,计算所有神经元和样本 x 的欧式距离,选距离最近的神经元作为获胜神经元 I。

选择与 x 距离最近的神经元 I
- 找到获胜神经元 I 后,需要更新神经元 I 和其邻居节点 (即拓扑结构上的邻居) 的特征向量 w 值,更新的时候有更新权重,越靠近 I 的神经元更新权重越大。对于神经元 j,其更新权重可以用下面的公式计算:

神经元 j 的更新权重
- 得到更新权重后,可以更新神经元的特征向量 w。更新的公式如下,主要是把特征向量往 x 的方向移动。

更新神经元的特征向量
训练完成后,输出层的神经元可以按照联系的紧密程度划分为几个部分,每部分代表一个簇或者一个类,如下图所示:

训练完成后,神经元可以划分为不同的簇
4.用 RSOM 求解 TSP
RSOM (Ring SOM) 是一种特殊的 SOM 网络,和上面说的 SOM 主要有两个区别:
- RSOM 输出层的神经元拓扑结构是环形的。
- 输出层神经元个数不是固定的,会随着训练不断增加神经元。
RSOM 的结构如下所示:
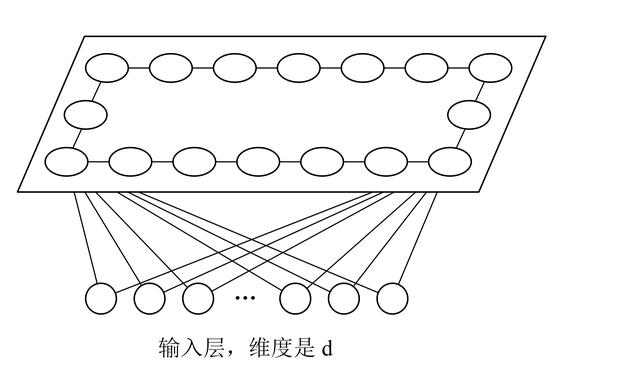
RSOM 示意图
RSOM 训练时的超参数包括:Tint (每更新 Tint 次,就在输出层插入一个新的神经元),Tmax (最大的训练次数),N(t) (t 时刻神经元的总个数),Ci(t) (t 时刻神经元 i 获胜的次数)。RSOM 训练过程如下:
- 随机初始化 N(0) 个神经元,所有神经元的计数 Ci(0) = 0。
- 对于一个输入 x,使用欧氏距离找出获胜神经元 I。
- 更新神经元 I 及其邻居节点的特征向量。
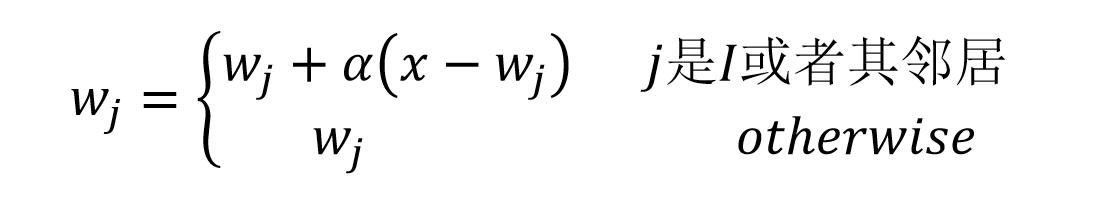
更新获胜神经元及其邻居的特征向量
- 获胜神经元的计数器 CI(t) 加 1,其邻居不用加。
- 如果更新了 Tint 次,则需要增加一个新的节点,新的节点在获胜神经元和其邻居之间添加。获胜神经元 I 有左右两个邻居 (因为环形的),选择距离远的邻居 f,并在 I 和 f 中间添加新神经元 r。新神经元 r 的特征向量是 I 和 f 特征向量的均值,同时修改新神经元 r 和获胜神经元 I 的计数器:
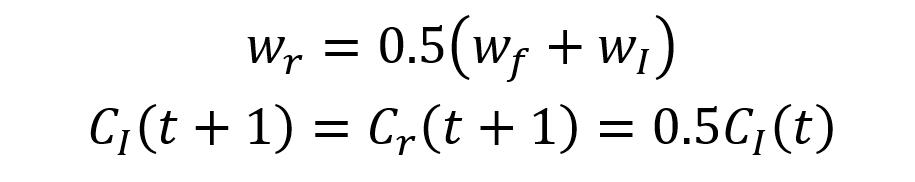
新神经元 r 的特征向量和计数器值
通过上面的步骤即可训练 RSOM 网络,在求解 TSP 问题时,输入样本 x 就是城市的坐标 (一般是 2 维,包含 x,y),每个神经元的特征向量维度也是 2。训练时每个城市都会找出一个获胜神经元,然后把该神经元及其邻居都拉向城市的坐标。可以理解为有个橡皮筋,每个城市把橡皮筋往自己的方向拉,最终橡皮筋上的不同点会固定到不同的城市中,如下图所示。

RSOM 求解 TSP 示意图
上图中的黑色点代表城市,白色点代表神经元,红色点代表获胜神经元。
5.参考文献
A simple learning algorithm for growing ring SOM and its Application to TSP























