导读：在大数据时代，对复杂数据结构中的各数据项进行有效的排序和查找的能力非常重要，因为很多现代算法都需要用到它。在为数据恰当选择排序和查找策略时，需要根据数据的规模和类型进行判断。尽管不同策略最终得到的结果完全相同，但使用恰当的排序和查找算法才能高效解决实际问题。

作者：伊姆兰·艾哈迈德（Imran Ahmad）

来源：华章科技

 

本文介绍以下排序算法：

• 冒泡排序（bubble sort）
• 归并排序（merge sort）
• 插入排序（insertion sort）
• 希尔排序（shell sort）
• 选择排序（selection sort）

01 在Python/ target=_blank class=infotextkey>Python中交换变量

在实现排序和查找算法时，需要交换两个变量的值。在Python中，有一种简单的方法可以交换两个变量，如下所示：

var1 = 1
var2 = 2
var1,var2 = var2,var1

print(var1,var2)

我们看看交换的结果。

2 1

本文的所有排序算法中都使用这种简单的方法来交换变量值。

下面我们从冒泡排序开始学习。

02 冒泡排序

冒泡排序是所有排序算法中最简单且最慢的一种算法，其设计方式是：当算法迭代时使得列表中的最大值像气泡一样冒到列表的尾部。由于其最坏时间复杂度是O(N2)，如前所述，它应该用于较小的数据集。

• 理解冒泡排序背后的逻辑

冒泡排序基于各种迭代（称为遍历）。对于大小为N的列表，冒泡排序将会进行N–1轮遍历。我们着重讨论第一次迭代，也就是第一轮遍历。

第一轮遍历的目标是将最大值移动到列表的尾部。第一轮遍历完成时，我们将看到列表中的最大值冒到了尾部。

冒泡排序会比较两个相邻变量的值，如果较低位置的变量值大于较高位置的变量值，则交换这两个值。这种迭代一直持续到我们到达列表的末尾，如图3-2所示。

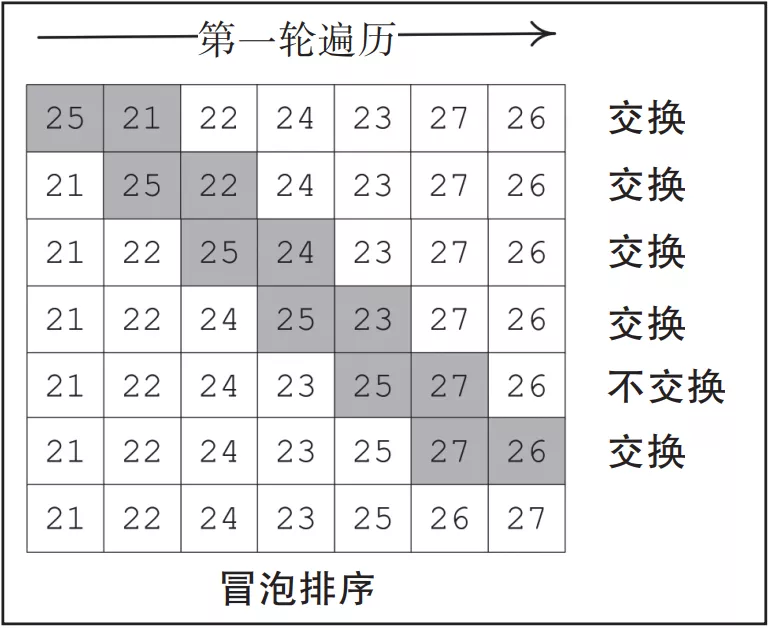
▲图 3-2

现在，我们看看如何使用Python实现冒泡排序：

#Pass 1 of Bubble Sort
lastElementIndex = len(list)-1
print(0,list)
for idx in range(lastElementIndex):
if list[idx]>list[idx+1]:
list[idx],list[idx+1]=list[idx+1],list[idx]
print(idx+1,list)

在Python中实现冒泡排序的第一轮遍历后，结果如图3-3所示。

▲图 3-3

一旦第一轮遍历完成，最大值就已经位于列表的尾部。算法接下来将进行第二轮遍历，第二轮遍历的目标是将第二大的值移动到列表第二高的位置。为此，算法将再次比较相邻变量的值，如果它们未按照大小排列则进行交换。第二轮遍历将跳过列表顶部元素，因为该元素在第一轮遍历后已经被放在了正确的位置上，因此不需要再移动。

完成第二轮遍历后，算法将继续执行第三轮遍历，以此类推，直到列表中的所有数据都按照升序排列。该算法将需要N–1轮遍历才能将大小为N的列表完全排序。Python中冒泡排序的完整实现如下所示。

def BubbleSort(list):
# Excahnge the elements to arrange in order
lastElementIndex = len(list)-1
for passNo in range(lastElementIndex,0,-1):
for idx in range(passNo):
if list[idx]>list[idx+1]:
list[idx],list[idx+1]=list[idx+1],list[idx]
return list

现在，我们看看冒泡排序算法的性能。

• 冒泡排序的性能

很容易就可以看出冒泡排序包含了两层循环：

• 外层循环：外层循环称为遍历。例如，第一轮遍历就是外层循环的第一次迭代。
• 内层循环：在每次内层循环的迭代过程中，对列表中剩余的未排序元素进行排序，直到最高值冒泡到右侧为止。第一轮遍历将进行N–1次比较，第二轮遍历将进行N–2次比较，而每轮后续遍历将减少一次比较操作。

由于存在两层循环，最坏情况下的运行时复杂度是O(n2)。

03 插入排序

插入排序的基本思想是，在每次迭代中，都会从数据集中移除一个数据点，然后将其插入到正确的位置，这就是为什么将其称为插入排序算法。

在第一次迭代中，我们选择两个数据点，并对它们进行排序，然后扩大选择范围，选择第三个数据点，并根据其值找到正确的位置。该算法一直进行到所有的数据点都被移动到正确的位置。这个过程如图3-5所示。

▲图 3-5

插入排序算法的Python代码如下所示：

def InsertionSort(list):
for i in range(1, len(list)):
j = i-1
element_next = list[i]
while (list[j] > element_next) and (j >= 0):
list[j+1] = list[j]
j=j-1
list[j+1] = element_next
return list

请注意，在主循环中，我们在整个列表中进行遍历。在每次迭代中，两个相邻的元素分别是list[j]（当前元素）和list[i]（下一个元素）。

在list[j]>element_next且j>=0时，我们会将当前元素与下一个元素进行比较。

我们使用此代码对数组进行排序。

list = [25,26,22,24,27,23,21]

InsertionSort(list)
print(list)

结果：

[21,22,23,24,25,26,27]

我们看一下插入排序算法的性能。

从算法的描述中可以明显看出，如果数据集已经排好序，那么插入排序将执行得非常快。事实上，如果数据集已经排好序，则插入排序仅需线性运行时间，即O(n)。最糟糕的情况是，每次内层循环都要移动列表中的所有元素。如果内层循环由i定义，则插入排序算法的最坏时间复杂度由以下公式给出：

 

总的遍历次数如图3-7所示。

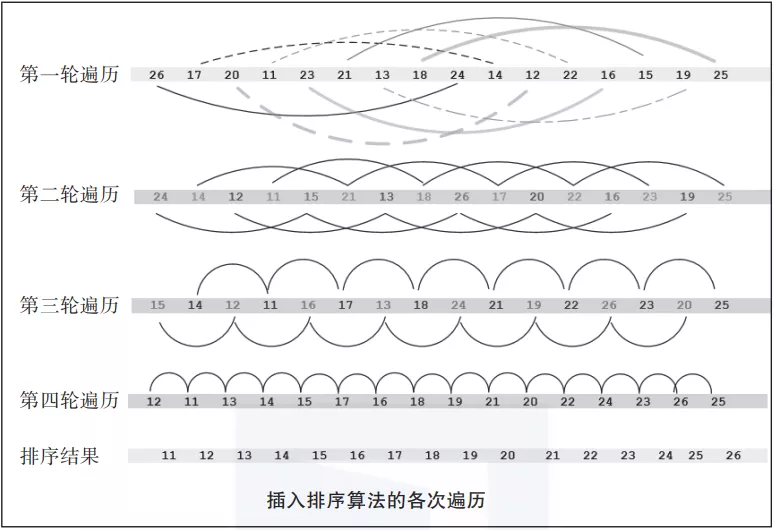
▲图 3-7

一般来说，插入排序可以用在小型数据集上。对于较大的数据集，由于其平均性能为平方级，不建议使用插入排序。

04 归并排序

到目前为止，我们已经介绍了两种排序算法：冒泡排序和插入排序。如果数据是部分有序的，那么它们的性能都比较好。本文讨论的第三种算法是归并排序算法，它是由约翰·冯·诺依曼（John von Neumann）在20世纪40年代开发的。该算法的主要特点是，其性能不取决于输入数据是否已排序。

同MapReduce和其他大数据算法一样，归并排序算法也是基于分治策略而设计的。在被称为划分的第一阶段中，算法将数据递归地分成两部分，直到数据的规模小于定义的阈值。在被称为归并的第二阶段中，算法不断地进行归并和处理，直到得到最终的结果。该算法的逻辑如图3-8所示。

▲图 3-8

我们先来看看归并排序算法的伪代码：

 

可以看到，该算法有以下三个步骤：

1. 它将列表划分为两个长度相等的部分。
2. 它使用递归来进行划分，直到每个列表的长度为1。
3. 它将有序的部分归并成一个有序的列表并返回。

归并排序算法的实现代码如下所示。

def MergeSort(list):
if len(list)>1:
mid = len(list)//2 #splits list in half
left = list[:mid]
right = list[mid:]

MergeSort(left) #repeats until length of each list is 1
MergeSort(right)

a = 0
b = 0
c = 0
while a < len(left) and b < len(right):
if left[a] < right[b]:
list[c]=left[a]
a = a + 1
else:
list[c]=right[b]
b = b + 1
c = c + 1
while a < len(left):
list[c]=left[a]
a = a + 1
c = c + 1

while b < len(right):
list[c]=right[b]
b = b + 1
c = c + 1
return list

运行前面的Python代码时，会产生一个对应的输出结果，如下所示。

list = [44,16,83,7,67,21,34,45,10]
MergeSort(list)
print(list)

[7, 10, 16, 21, 34, 44, 45, 67, 83]

可以看到，该代码执行后的输出结果是一个有序列表。

05 希尔排序

冒泡排序算法比较相邻的元素，如果它们不符合顺序，则进行交换。如果我们有一个部分有序的列表，则冒泡排序应该能够给出比较合理的性能，因为一旦循环中不再发生元素交换，冒泡排序就会退出。

但是对于一个规模为N的完全无序的列表，冒泡排序必须经过N–1次完整的迭代才能得到完全排好序的列表。

丹诺德·希尔（Donald Shell）提出了希尔排序（以他的名字命名），该算法质疑了对选择相邻的元素进行比较和交换的必要性。

现在，我们来理解这个概念。

在第一轮遍历中，我们不选择相邻的元素，而是选择有固定间距的两个元素，最终排序出由一对数据点组成的子列表，如图3-11所示。在第二轮遍历中，对包含四个数据点的子列表进行排序（见图3-11）。

▲图 3-11

在后续的遍历中，每个子列表中的数据点数量不断增加，子列表的数量不断减少，直到只剩下一个包含所有数据点的子列表为止。此时，我们可以认为列表已经排好序了。

在Python中，用于实现希尔排序算法的代码如下：

def ShellSort(list):
distance = len(list) // 2
while distance > 0:
for i in range(distance, len(list)):
temp = list[i]
j = i
# Sort the sub list for this distance
while j >= distance and list[j - distance] > temp:
list[j] = list[j - distance]
j = j-distance
list[j] = temp
# Reduce the distance for the next element
distance = distance//2
return list

用前面的代码对列表进行排序，结果如下所示。

list = [26,17,20,11,23,21,13,18,24,14,12,22,16,15,19,25]
ShellSort(list)
print(list)

[11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]

可以看到，调用ShellSort函数成功地对输入数组进行了排序。

• 希尔排序的性能

希尔排序并不适用于大数据集，它用于中型数据集。粗略地讲，它在一个最多有6000个元素的列表上有相当好的性能，如果数据的部分顺序正确，则性能会更好。在最好的情况下，如果一个列表已经排好序，则它只需要遍历一次N个元素来验证顺序，从而产生O(N)的最佳性能。

06 选择排序

正如在本文前面所看到的，冒泡排序是最简单的排序算法。选择排序是对冒泡排序的改进，我们试图使得算法所需的总交换次数最小化。

与冒泡排序算法的N–1轮遍历过程相比，选择排序在每轮遍历中仅产生一次交换，在每轮遍历中寻找最大值并将其直接移动到尾部，而不是像冒泡排序那样，每轮遍历都一步一步地将最大的值向尾部移动。因此，在第一轮遍历后，最大值位于列表尾部。在第二轮遍历后，第二大的值会紧邻最大值。

随着算法的进行，后面的值将根据它们的大小移动到正确的位置。最后一个值将在第N–1轮遍历后移动。因此，选择排序同样需要N–1轮遍历才能对N个数据项进行排序（如图3-13所示）。

▲图 3-13

这里展示了选择排序在Python中的实现：

def SelectionSort(list):
for fill_slot in range(len(list) - 1, 0, -1):
max_index = 0
for location in range(1, fill_slot + 1):
if list[location] > list[max_index]:
max_index = location
list[fill_slot],list[max_index] = list[max_index],list[fill_slot]
return list

执行选择排序算法时，将产生如下所示的输出。

list = [70,15,25,19,34,44]
SelectionSort(list)
print(list)

[15,19,25,34,44,70]

可以看到，最后的输出结果就是排好序的列表。

• 选择排序的性能

选择排序的最坏时间复杂度是O(N2)。请注意，其最坏性能近似于冒泡排序的性能，因此不应该用于对较大的数据集进行排序。不过，选择排序仍是比冒泡排序设计更好的算法，由于交换次数减少，其平均复杂度比冒泡排序好。

小结：选择一种排序算法

恰当地选择排序算法既取决于当前输入数据的规模，也取决于当前输入数据的状态。对于已经排好序的较小的输入列表，使用高级算法会给代码带来不必要的复杂度，而性能的提升可以忽略不计。

例如，对于较小的数据集，我们不需要使用归并排序，冒泡排序更容易理解和实现。如果数据已经被部分排好序了，则可以使用插入排序。对于较大的数据集，归并排序算法是最好的选择。

关于作者：伊姆兰·艾哈迈德（Imran Ahmad） 是一名经过认证的谷歌讲师，多年来一直在谷歌和学习树(Learning Tree)任教，主要教授Python、机器学习、算法、大数据和深度学习。他在攻读博士学位期间基于线性规划方法提出了名为ATSRA的新算法，用于云计算环境中资源的优化分配。近4年来，他一直在加拿大联邦政府的高级分析实验室参与一个备受关注的机器学习项目。

本文摘编自《程序员必会的40种算法》，经出版方授权发布。