数据库,你应该掌握的八种数据结构!
在互联网快速发展的今天,我们见证了现代数据库从结构化数据库(比如:MySQL)到 NoSQL(比如:redis),再到大型的分布式数据库(比如:Apache Cassandra),数据库之所以可以如此快速的发展,离不开这 8种关键的数据结构,如下图:
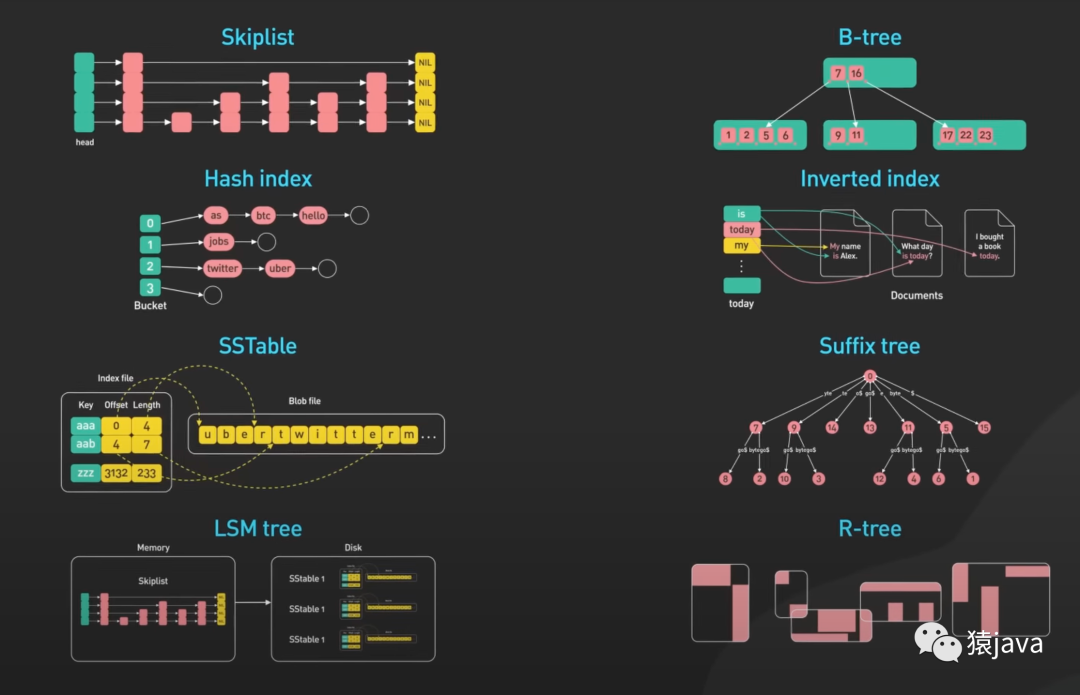
因此,今天我们就来聊一聊这 8种数据结构。
一、Skiplist
Skip List(跳表)是一种基于链表的数据结构,用于快速查找和插入操作。它是由William Pugh于 1989 年提出的,类似于平衡二叉树,但相对于平衡二叉树而言,跳表的实现更简单且容易理解,因此它是平衡树的替代品。
原理
- 跳表节点结构:每个跳表节点包含一个键(key)和一个值(value),以及多个指向下一层节点的指针(forward pointers)。节点按照键的递增顺序连接在一起,形成一种层级结构。
- 层级结构:跳表中的节点按照层级连接,最底层是一个普通的有序链表。每个节点都有一个或多个指针指向下一层节点,这些指针称为前进指针(forward pointers)。通常,节点的层数是随机生成的,层数越高,节点在跳表中的概率越小。
- 查找操作:从顶层开始,逐层比较节点的键和目标键的大小,如果当前节点的下一个节点的键大于目标键,则向下一层移动。重复这个过程直到找到目标键或者无法继续向下移动为止。一般来说,查找操作的时间复杂度为O(log n)。
- 插入操作:插入操作需要首先执行查找操作,以找到插入位置。然后,为新节点生成一个随机的层数,将新节点插入到每一层的合适位置,并更新相关节点的前进指针。插入操作的时间复杂度也是O(log n)。
- 删除操作:删除操作与查找操作类似,首先执行查找操作找到待删除的节点。然后,将待删除节点从每一层中移除,并更新相关节点的前进指针。删除操作的时间复杂度也是O(log n)。
跳表通过增加多个层级和前进指针的方式,提供了一种平衡的查找和插入性能。相较于平衡二叉树,跳表的实现更简单,且不需要维护复杂的平衡条件。如下图,给出一张跳表的示例图:
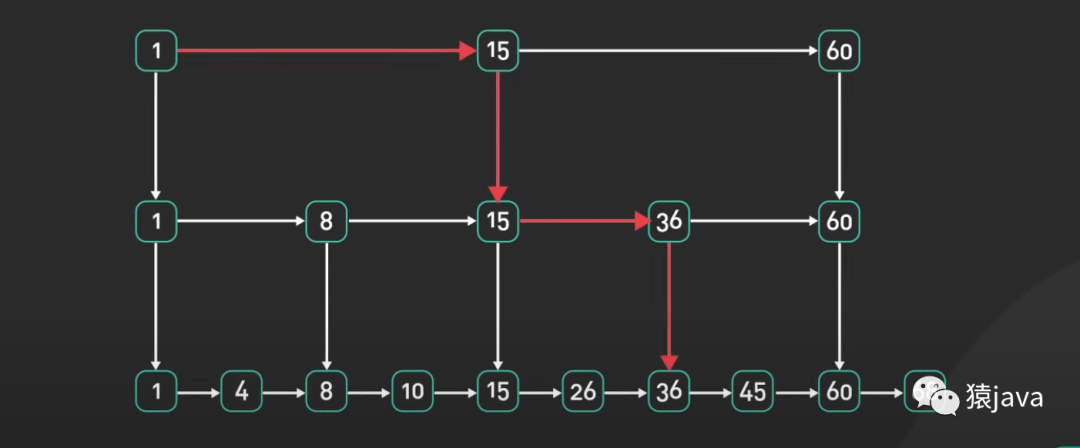
优缺点
跳表的优势在于其相对简单的实现和较高的查询性能。对于有序链表的查找操作,跳表平均时间复杂度为O(log n),接近于平衡树的性能,而且在实际应用中比平衡树更加容易实现和维护。然而,跳表的插入和删除操作的平均时间复杂度较高,为O(log n),相比于链表的O(1)操作略慢。
数据库实例
在 Redis这种内存数据库中,跳表用于实现有序数据结构,例如排序集和排序列表。
二、B-tree
B-tree(平衡树)是一种常用的自平衡搜索树,广泛应用于数据库系统和文件系统等领域,用于高效地组织和管理大量有序的数据。B-tree的原理如下:
原理
- 结构组成:B-tree由一个根节点、一系列的内部节点和叶子节点组成的多层树结构。每个节点包含一个键值列表和对应的子节点指针。内部节点的键值用于确定子节点的范围,叶子节点存储实际的数据。
- 平衡性:B-tree的特点之一是保持树的平衡性,即所有叶子节点具有相同的深度。通过保持树的平衡,可以确保在最坏情况下,对数据的查找、插入和删除操作具有良好的性能。
- 范围查询:B-tree支持范围查询,即查找满足给定范围条件的数据。查询从根节点开始,根据给定的范围条件选择相应的子节点。逐层向下遍历子节点,根据子节点的键值范围进一步选择子节点,直到到达叶子节点。在叶子节点中,按顺序检查每个键值是否满足范围条件,并返回符合条件的数据。
- 插入操作:插入数据时,B-tree先进行查找操作,找到应该插入的叶子节点。如果叶子节点未满,可以直接插入新的键值。如果叶子节点已满,则进行节点分裂操作。将当前节点的键值分成两个部分,左边的部分保留在当前节点,右边的部分形成一个新的叶子节点。同时,将分裂点的键值插入到父节点中,并调整父节点的指针。
- 删除操作:删除数据时,B-tree首先进行查找操作,找到要删除的键值所在的叶子节点。如果叶子节点中存在该键值,则直接删除。如果删除后叶子节点的键值数量低于最小阈值,可以进行一些修复操作,如兄弟节点的合并或重新分配键值。
下面给了一张B-tree 和 一张 B+tree 的示例图:
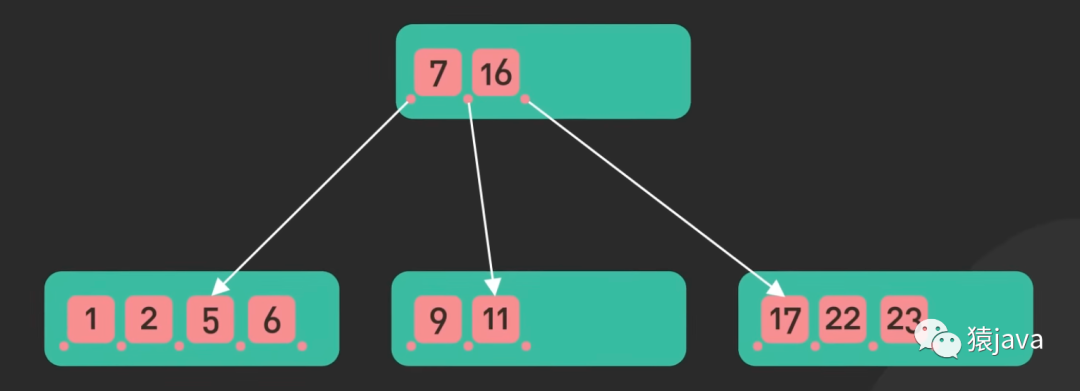
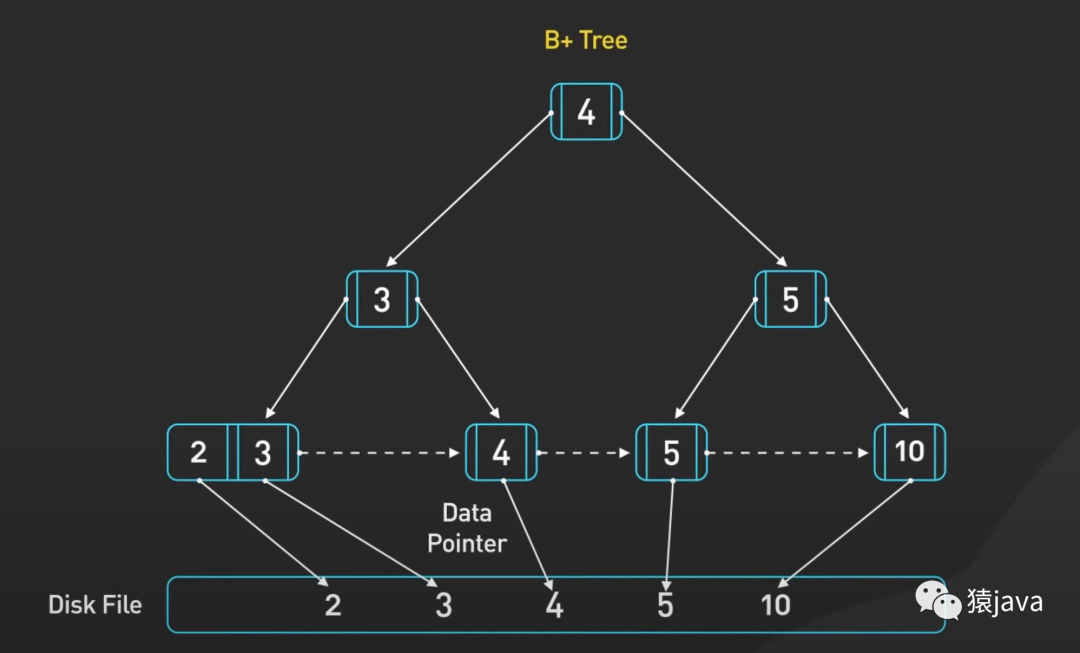
优缺点
B-tree的优点在于它对有序数据的高效组织和检索能力,能够在平衡性和高性能之间取得良好的平衡。它被广泛应用于数据库系统、文件系统和其他需要高效搜索和索引的场景中。B-tree的变种形式,如B+树和B*树,进一步优化了查询性能和磁盘访问效率,使其适用于处理大规模数据和支持范围查询等更复杂的操作。
数据库实例
在 MySQL 的InnoDB 引擎就是使用 B+Tree实现索引机制,Postgres 和 Oracle数据也是用B-Tree 来处理大量磁盘数据。
三、Hash index
哈希索引(Hash Index)是一种常用的索引结构,它通过哈希函数将索引键映射到索引桶(或槽)中,以实现快速的查找和访问。
原理
- 哈希函数:哈希索引利用哈希函数将索引键转换为一个固定长度的哈希值。哈希函数应该具备以下特点:快速计算、均匀分布、无冲突。
- 索引桶:哈希索引将所有可能的哈希值范围划分为多个索引桶。每个索引桶中存储了具有相同哈希值的索引键所对应的数据位置(如磁盘地址或内存地址)。
- 哈希冲突处理:由于哈希函数的输出范围可能小于实际的键值范围,因此会出现哈希冲突的情况,即不同的键经过哈希函数得到相同的哈希值。常见的哈希冲突处理方法包括拉链法(ChAIning)和开放寻址法(Open Addressing)。
- 拉链法:每个索引桶中维护一个链表(或其他数据结构),将哈希值相同的键值对链接在一起。当发生哈希冲突时,新的键值对可以添加到链表的末尾。
- 开放寻址法:当发生哈希冲突时,继续探测其他索引桶,直到找到一个空闲的索引桶。常见的探测方法有线性探测、二次探测、双重哈希等。
- 查找操作:对于查找操作,首先使用哈希函数计算给定索引键的哈希值,然后根据哈希值找到对应的索引桶。如果存在哈希冲突,则按照哈希冲突处理的方法进行搜索,直到找到目标键值对或者确定不存在。
- 插入操作:插入操作也需要使用哈希函数计算待插入键的哈希值,并找到对应的索引桶。根据哈希冲突处理的方法,将键值对插入到索引桶中的合适位置。
- 删除操作:删除操作类似于查找操作,根据哈希值找到对应的索引桶,然后在该索引桶中搜索目标键值对,并进行删除。
如下图,给出两张hash index的示例图:
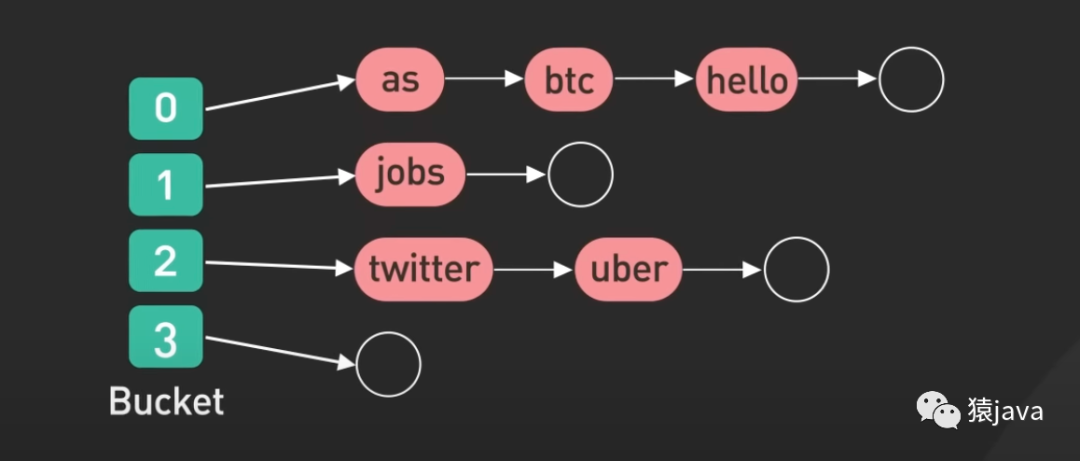
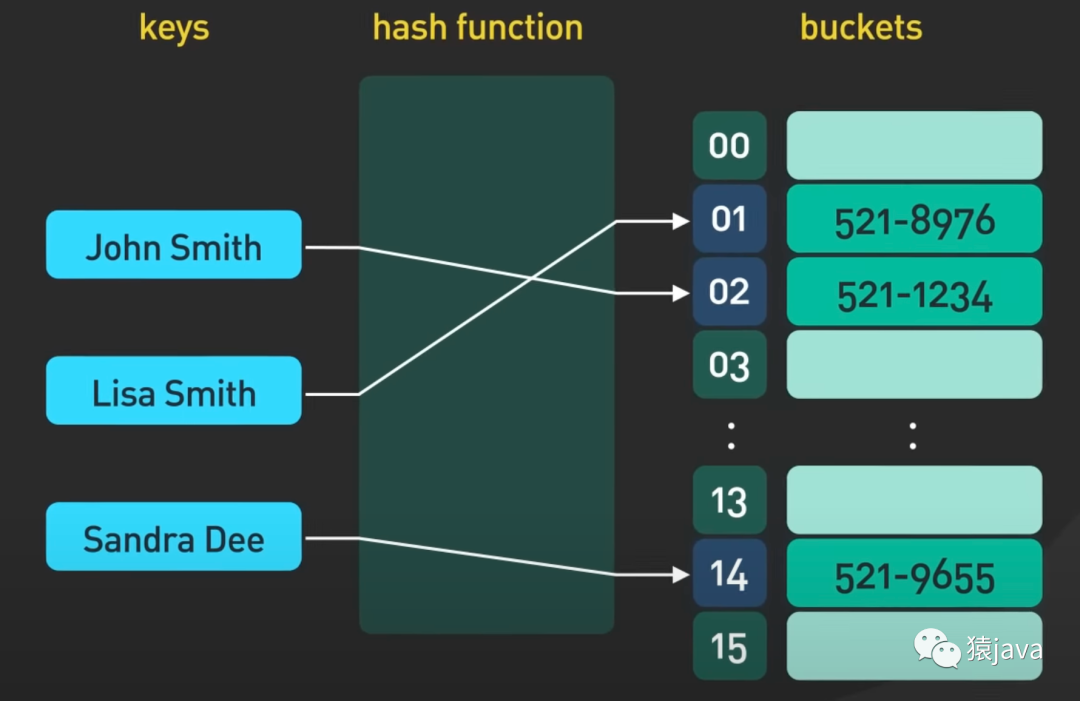
优缺点
优点:
- 快速查找:哈希索引通过哈希函数的映射,可以快速计算出目标键值对所在的索引桶,从而加快查找速度。
- 常数时间复杂度:在理想情况下,哈希索引的查找操作只需要常数时间复杂度O(1),即使在大数据集中也能保持较快的查询速度。
- 适合等值查找:哈希索引主要用于等值查找,对于需要精确匹配的查询非常高效。
缺点和局限性:
- 哈希冲突:由于哈希函数的输出范围有限,不同的键可能映射到相同的哈希值,导致哈希冲突。哈希冲突会影响查找性能,需要采用合适的哈希冲突处理方法,如拉链法或开放寻址法。
- 不支持范围查询:哈希索引只适用于等值查找,无法直接支持范围查询。范围查询需要遍历整个索引,效率较低。
- 哈希函数的选择:选择合适的哈希函数非常重要,一个好的哈希函数应具备均匀分布、快速计算和最小化冲突等特点,否则可能导致较多的哈希冲突,降低索引性能。
- 内存占用:哈希索引需要维护额外的索引结构,包括哈希桶和指针,相对于原始数据的存储,会占用更多的内存空间。
数据库实例
hash index 无处不在,它可以用来实现像 Redis 中的 Hashes 这样的哈希数据结构。
四、Inverted index
Inverted Index(倒排索引)是一种常用的索引结构,用于实现全文搜索和快速的关键词检索。它将文档集合中的每个单词或关键词映射到包含该单词的文档列表,以支持高效的倒排查找。
原理
- 文档收集:首先需要收集要建立索引的文档集合。文档可以是一篇文章、一本书或者是网页等,每个文档都有一个唯一的标识符,如文档ID。
- 分词处理:对于每个文档,需要进行分词处理。分词将文本划分为一个个单词或关键词,去除停用词(如“的”、“是”等)和标点符号,对词根进行处理(如词干提取、词形还原等),以获取关键词集合。
- 构建倒排索引:对于每个关键词,构建倒排索引表。倒排索引表中的每一项包含一个关键词和包含该关键词的文档列表。文档列表中记录了包含该关键词的文档ID或其他相关信息。倒排索引表按照关键词的字典序排列。
- 查询操作:当进行查询时,将查询的关键词进行分词处理,然后在倒排索引表中查找对应的关键词。根据倒排索引表中的文档列表,可以快速找到包含查询关键词的文档集合。
- 结果排序:根据查询的相关性,对匹配的文档进行排序,以确定搜索结果的排名。相关性可以根据不同的算法和评分模型进行计算,如TF-IDF、BM25等。
下面给出了一张Inverted index的示例图:
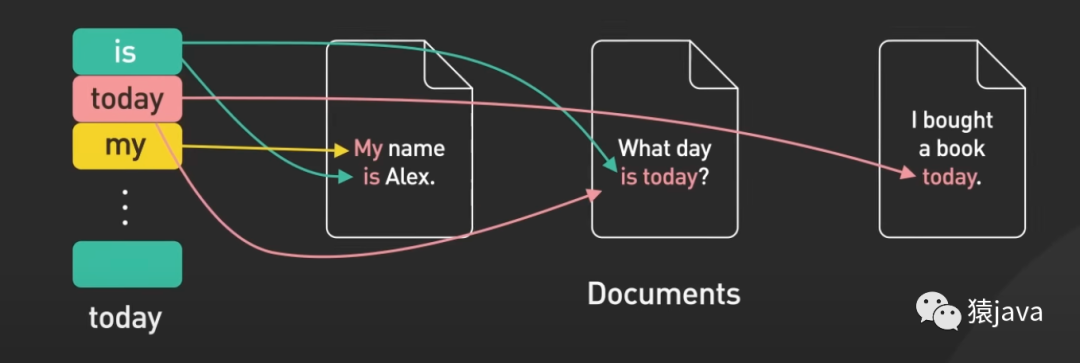
优缺点
倒排索引的优点是可以快速定位包含特定关键词的文档,适用于全文搜索和关键词检索场景。它具有较高的查询效率,能够快速过滤不相关的文档,提供精确的搜索结果。同时,倒排索引支持动态更新,可以方便地添加、删除或修改文档。
然而,倒排索引也有一些局限性,如占用较多的存储空间,需要维护索引结构和更新索引等。为了解决这些问题,通常会采用压缩技术、索引合并和分布式索引等策略来提高存储效率和查询性能。
总结起来,倒排索引通过将关键词映射到包含该关键词的文档列表,实现了高效的全文搜索和关键词检索
数据库实例
倒排索引最典型的使用就是 ElasticSearch,用于全文检索。
五、SSTable
SSTable(Sorted String Table)是一种常用的存储结构,用于实现高效的键值存储和检索。它是 google 的 Bigtable 论文中提出的一种数据结构,是 LSM-tree的核心组件。
原理
- 数据排序:SSTable中的数据按照键的有序排列,通常以字典序为准。这样做的好处是可以支持范围查询和快速查找。数据排序可以在内存中进行,也可以在写入时进行排序。
- 数据存储:SSTable将有序的键值对按照一定的规则存储到磁盘上的文件中。每个文件包含多个数据块(Data Block),每个数据块包含多个键值对。
- 索引结构:为了快速定位数据块和具体的键值对,SSTable维护了一个索引结构,通常称为Block Index或Data Block Index。索引中存储了每个数据块的起始位置、结束位置和该块中最小键值对的键。
- 写入操作:当写入一个新的键值对时,首先会将键值对追加到内存中的MemTable中(通常是跳表或红黑树等数据结构)。当MemTable达到一定大小后,会触发数据的刷写操作。将MemTable中的键值对按照键的顺序写入到磁盘上的SSTable文件中,并更新索引结构。
- 读取操作:当执行读取操作时,首先在内存中的MemTable中查找键值对。如果未找到,则依次在磁盘上的SSTable文件中的索引结构中进行查找,定位到对应的数据块,然后在该数据块中进行查找具体的键值对。
- 合并操作:为了减少SSTable文件数量和提高读取性能,周期性地执行合并操作。合并操作将多个SSTable文件合并成一个更大的文件,同时更新索引结构。合并时会进行去重和排序操作,以消除重复的键和更新过期的键。
下面给出了一张 SSTable 的示例图:
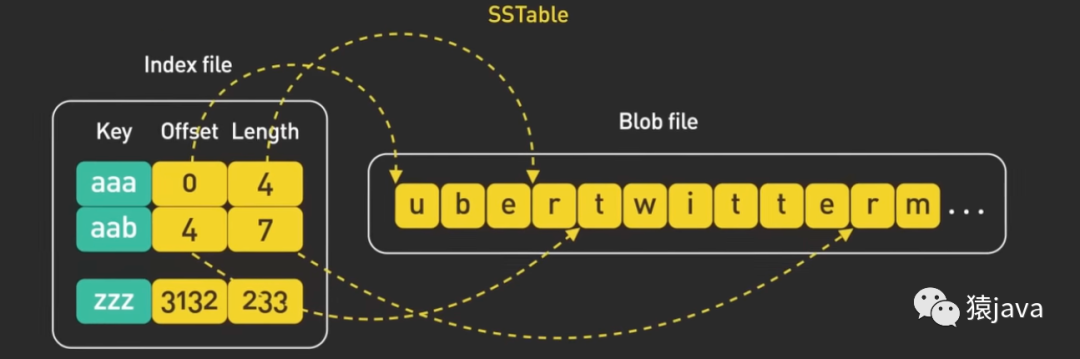
优缺点
SSTable的优点是具有高效的查询性能和压缩存储,适用于读多写少的场景。由于数据有序存储,支持范围查询和快速查找。此外,SSTable还支持持久化存储和数据恢复,即使在系统故障或重启后也能保持数据的完整性。
SSTable也有一些局限性,如合并操作可能会引起写放大(Write Amplification)问题,当需要合并的文件过多时,会影响性能。为了解决这个问题,可以采用类似于LevelDBLevelDB等SSTable实现的系统采用了多层次的SSTable结构,如Level-0、Level-1、Level-2等,通过不同的层次来解决写放大的问题。具体的机制如下:
- 层次结构:LevelDB等系统通常采用多层次的SSTable结构。Level-0是最底层的SSTable,数据按照写入的顺序存储,并且不进行合并操作。Level-1及以上的层次则是合并Level-0层的SSTable文件得到的新SSTable文件。
- 合并策略:合并操作在不同的层次上执行,每个层次都有自己的合并策略。通常,Level-0的合并操作由后台线程异步执行,目的是将多个小的SSTable文件合并为一个较大的SSTable文件,减少文件数量。而Level-1及以上的合并操作由前台线程同步执行,以控制合并的规模和频率。
- 划分文件大小:不同层次的SSTable文件有不同的大小限制。通常,Level-0的文件较小,可以存储较少的数据;而随着层次的增加,文件的大小逐渐增大。这样做的目的是确保在合并操作时,每个层次的文件规模适中,不会导致过大的写放大问题。
- 基于时间和大小的触发条件:合并操作的触发可以基于时间和文件大小两个条件。根据时间条件,可以设置合并操作的触发间隔,如每隔一段时间执行一次合并;根据大小条件,可以设置Level-0中SSTable文件的最大大小,当文件达到阈值时触发合并操作。
通过多层次的SSTable结构和合并策略,LevelDB等系统能够平衡写放大和查询性能。较小的Level-0文件数量减少了写放大的问题,同时较大的Level-1及以上文件减少了查询时需要扫描的SSTable文件数量,提高了读取性能。这种层次结构和合并策略的设计使得LevelDB等系统适用于高效的键值存储和检索场景。
数据库实例
SSTable 被广泛应用于多个系统中,如LevelDB、RocksDB等。
六、LSM-Tree
LSM-Tree(Log-Structured Merge Tree)是一种常用的数据结构,用于实现高效的键值存储和检索。它将写入操作与合并操作分离,通过将数据写入日志文件和内存缓存,然后定期进行合并操作来提高写入和查询的性能。
原理
(1) 写入操作:
- 写入日志文件(Write-Ahead Log, WAL):当有新的键值对需要写入时,首先将其追加到顺序写的日志文件中。这个操作称为写前日志(Write-Ahead Logging),它可以确保数据的持久性和一致性。
- 写入内存缓存(Memtable):同时将新的键值对写入内存中的数据结构,通常是跳表或红黑树等有序数据结构。内存缓存可以快速响应读取操作,并且具有较高的写入性能。
(2) 合并操作:
- 内存与磁盘的合并(Memtable to SSTable):当内存缓存达到一定大小或者其他触发条件满足时,将内存缓存中的键值对写入到磁盘上的SSTable(Sorted String Table)文件中,通常以一种有序的方式进行存储。
- SSTable的合并:定期或根据其他策略执行SSTable文件的合并操作。合并操作将多个SSTable文件进行合并,消除重复键和更新过期键,并生成新的SSTable文件。合并操作可以基于时间、文件大小或其他条件进行触发和控制。
(3) 查询操作:
- 内存缓存查询:首先在内存缓存中查找键值对,由于内存缓存是有序的,可以快速定位。
- 磁盘上的SSTable查询:如果在内存缓存中未找到,则依次在磁盘上的SSTable文件中进行查找,通常采用二分查找等算法进行快速定位和检索。
下面给出了一张 LSM-tree的示例图:

优缺点
LSM树的优点是具有较高的写入性能和压缩存储,适用于写多读少或写入速度较快的场景。通过将写入操作集中在内存和顺序写的日志文件中,可以获得较高的写入吞吐量。查询性能也较好,通过内存缓存和有序的SSTable文件,可以快速定位和检索键值对。
然而,LSM树也有一些局限性,如读取操作可能需要扫描多个SSTable文件,导致查询性能不如B树等结构稳定。此外,合并操作可能会引起较长的停顿时间,对于实时性要求较高的系统可能会有影响。为了解决这些问题,LSM树引入了一些优化技术,如布隆过滤器和层级结构。
- 布隆过滤器(Bloom Filter):LSM树中的每个SSTable文件可以关联一个布隆过滤器。布隆过滤器是一种高效的概率型数据结构,用于快速判断某个键是否存在于SSTable文件中,从而避免不必要的磁盘访问。布隆过滤器可以在非常低的误判率下,快速准确地判断某个键是否可能存在于SSTable文件中。
- 层级结构:LSM树通常包含多个层级,如Level-0、Level-1、Level-2等。Level-0是内存缓存和日志文件,Level-1及以上是磁盘上的SSTable文件。较小的层级(如Level-0)通常用于高频的写入操作,较大的层级(如Level-1及以上)用于存储稳定的数据。通过层级结构,可以减少查询时需要扫描的SSTable文件数量,提高读取性能。
- 压缩和合并策略:LSM树可以采用不同的压缩算法和合并策略来优化存储和性能。例如,可以使用压缩算法对SSTable文件进行压缩,减少磁盘占用空间。合并策略可以根据不同的触发条件和优先级,灵活地控制合并操作的频率和规模,以平衡写入性能和查询性能。
数据库实例
LSM-tree 是 Apache Cassandra、RocksDB 和 LevelDB 等流行的 NoSQL 数据库的支柱。
七、Suffix tree
Suffix Tree(后缀树)是一种用于处理字符串的数据结构,它能够高效地存储一个字符串的所有后缀,并支持快速的子串匹配和搜索操作。
原理
- 构建树结构:Suffix Tree是由一个根节点和一系列的内部节点和叶子节点组成的树结构。根节点没有入边,每个内部节点代表一个非空字符串的前缀,叶子节点代表原始字符串的后缀。每个节点通过边连接,边上的标记代表了字符串的字符。
- 后缀链接(Suffix Link):为了提高构建和搜索的效率,Suffix Tree中的每个内部节点都可以包含一个后缀链接,指向具有相同前缀的下一个内部节点。后缀链接能够在搜索过程中跳跃到下一个具有相同前缀的位置,加速匹配操作。
- 自动构建:Suffix Tree的构建算法使用了称为Ukkonen算法的在线构建方法。它通过逐步将字符添加到树中来构建树结构,而不是一次性将整个字符串添加进去。Ukkonen算法的核心思想是通过在树的每一步添加新字符,不断扩展现有的节点或添加新的节点,同时维护后缀链接,以保持树的正确性。
- 字符串匹配:通过Suffix Tree可以高效地进行子串匹配和搜索操作。给定一个模式字符串,可以从根节点开始,依次匹配模式中的字符,并沿着相应的边移动。如果无法匹配当前字符,则搜索失败;如果成功匹配,则继续匹配下一个字符,直到匹配完成。这样可以在时间复杂度为O(m)的情况下完成匹配,其中m是模式字符串的长度。
下面给出了一张 Suffix-tree的示例图:
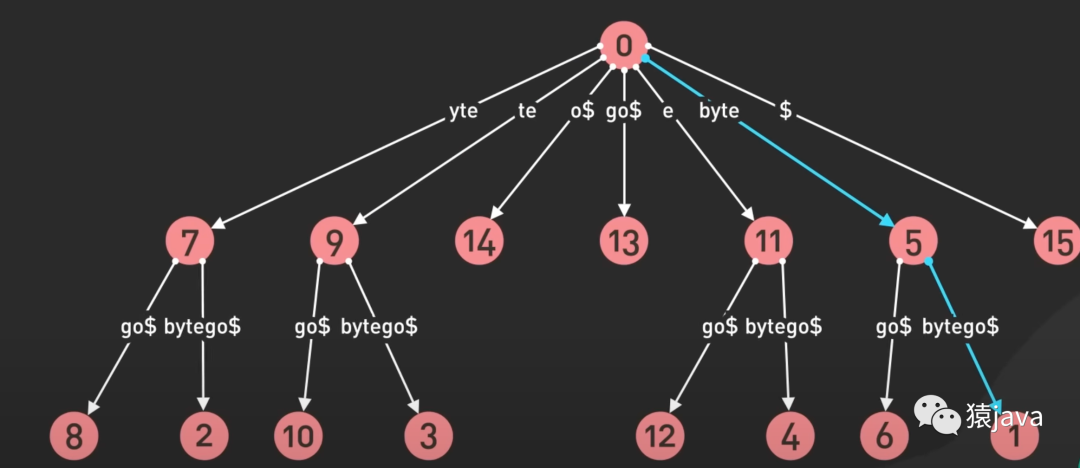
优缺点
Suffix Tree是一种非常强大和高效的数据结构,可以用于解决各种字符串处理问题,如子串查找、最长公共子串、重复子串等。它在文本搜索、基因组学、自然语言处理等领域都有广泛的应用。然而,构建Suffix Tree的算法相对复杂,需要高效的实现才能处理大规模的字符串。因此,一些改进的变体如Suffix Array和压缩后缀树也得到了广泛的研究和应用。
数据库实例
PostgreSQL、Apache Lucene 和 Elasticsearch、Riak
八、R-tree
R-tree是一种常用的数据结构,用于高效地组织和检索多维空间数据,特别是用于范围查询和最近邻查询。
原理
- 结构组成:R-tree是由一个根节点和一系列的内部节点和叶子节点组成的树结构。每个节点代表一个矩形区域,内部节点的矩形区域覆盖了其子节点的矩形区域,而叶子节点代表了具体的数据对象和其对应的矩形区域。
- 节点的填充和分裂:为了保持树的平衡和高效性能,R-tree在节点的填充和分裂时采用一些策略。节点的填充策略使得节点尽可能充满数据对象,避免空间浪费。当节点无法再容纳新的数据对象时,节点将会被分裂成两个更小的节点,以容纳新的数据对象。
- 范围查询:R-tree支持范围查询,即查找所有与给定查询矩形区域相交的数据对象。查询从根节点开始,逐层向下遍历,对于每个遇到的节点,检查该节点的矩形区域是否与查询区域相交。如果相交,则继续向下遍历其子节点;如果不相交,则跳过该节点及其子节点。通过这种方式,可以逐步缩小搜索范围,找到所有满足查询条件的数据对象。
- 最近邻查询:R-tree也支持最近邻查询,即查找与给定点最接近的数据对象。查询从根节点开始,根据给定点与节点的距离进行排序,优先访问最接近给定点的节点。在访问节点时,继续向下遍历其子节点,并根据给定点与子节点的距离进行排序。通过这种方式,可以逐步接近最近邻数据对象,直到找到最接近的数据对象或达到预设的搜索范围。
下面给出了一张 R-tree的示例图:
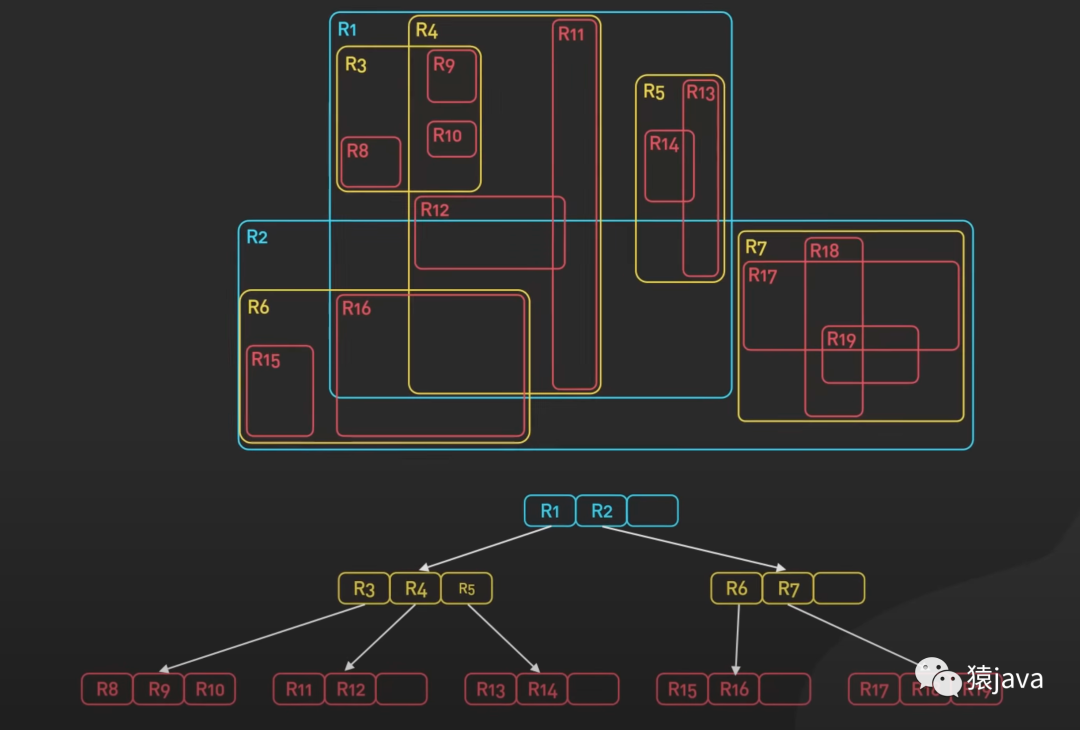
优缺点
R-tree的优点在于它对多维空间数据的高效组织和查询。通过逐层的树结构和节点分裂策略,R-tree可以有效地减少不必要的搜索范围,提高查询性能。它被广泛应用于地理信息系统(GIS)、数据库系统、图像处理和空间数据索引等领域,用于支持高效的空间数据管理和检索需求。
数据库实例
PostGIS、MongoDB 和 Elasticsearch。