刷了360多道算法题,我终于顿悟了它的真谛
最近一直在刷算法题,刷华为OD算法题,有诸多好处:
- 比如可以考华为OD岗位,大厂算法岗,待遇直接拉满,走向人生巅峰。
- 不考也没关系,就当练习算法题了,哪吒半年时间刷了360多道题,平均一天六道题,一道题40分钟,一天刷4个小时?现在一看到算法题,真的有一种灵光乍现的感觉。
希望用我自己疯狂刷题的劲头,感染大家,让大家爱上刷题,顺利通过华为OD机试,掌握更多优秀的算法。
下面这道题,是很经典的深度优先搜索dfs算法 + 二叉树。掌握一道题,精通一类题,冲吧~
一、题目描述
某文件系统中有N个目录,每个目录都有一个独一无二的ID。每个目录只有一个父目录,但每个父目录下可以有零个或者多个子目录,目录结构呈树状结构。
假设,根目录的ID为0,且根目录没有父目录,其他所有目录的ID用唯一的正整数表示,并统一编号。
现给定目录ID和其父目录ID的对应父子关系表[子目录ID,父目录ID],以及一个待删除的目录ID,请计算并返回一个ID序列,表示因为删除指定目录后剩下的所有目录,返回的ID序列以递增序输出。
注意:
- 被删除的目录或文件编号一定在输入的ID序列中。
- 当一个目录删除时,它所有的子目录都会被删除。
说人话就是:
输入m行数据,第一个元素是子节点值,第二个是父节点值,m行数据可以组成一个二叉树。
最后输入要删除的节点,求二叉树剩下的节点值。
例如输入:
5
8 6
10 8
6 0
20 8
2 6
8
二叉树就会变为:
6
2 8
10 20
删除最后的8,输出6 2就是结果。
很简单吧,少年~
二、输入描述
输入的第一行为父子关系表的长度m;
接下来的m行为m个父子关系对;
最后一行为待删除的ID。序列中的元素以空格分割。
三、输出描述
输出一个序列,表示因为删除指定目录后,剩余的目录ID。
四、深度优先搜索dfs
1、搜索的要点:
- 初始状态。
- 重复产生新状态。
- 检查新状态是否为目标,是结束,否转(2)。
如果搜索是以接近起始状态的程序依次扩展状态的,叫宽度优先搜索。
2、如果扩展是首先扩展新产生的状态,则叫深度优先搜索。
深度优先搜索用一个数组存放产生的所有状态。
- 把初始状态放入数组中,设为当前状态。
- 扩展当前的状态,产生一个新的状态放入数组中,同时把新产生的状态设为当前状态。
- 判断当前状态是否和前面的重复,如果重复则回到上一个状态,产生它的另一状态。
- 判断当前状态是否为目标状态,如果是目标,则找到一个解答,结束算法。
- 如果数组为空,说明无解。
3、深度优先搜索dfs代码架构:
public int def(int x, int y ,int step){
if(递归出口/达到目标状态){
//进行对应操作
return 0;
}
for (int i = 0; i < n; i++) {
//遍历剩下的所有的情况
if(visit[i]==0){
//未访问
x = 下一步更新;
y = 下一步更新;
visit[i] = 1;
def(x,y,step);
visit[i] = 0; //记得回溯还原
}
}
}
五、解题思路
根据题目描述,输入数据可以组成一个二叉树,如果将某个节点删除,求剩余节点。
输入父子关系表的长度m。
接下来的m行输入父子关系。
输入待删除的ID。
遍历m个父子关系,拼接成二叉树,拼接剩余的目录ID。
- 如果该关系的父节点是value。
- 如果该父节点不是待移除的ID。
- 拼接成二叉树。
- 拼接剩余的目录ID -- builder。
- 移除满足条件的父子关系。
- 父子关系集合treeList移除某节点,treeList长度-1,下一个坐标i也应该-1。
- 如果剩余的父子关系集合treeList为0,则不需要再进行dfs,如果要dfs的node节点是null,则不需要再寻找其左右子节点;
- 遍历treeList,拼接二叉树。
在剩余的父子关系集合treeList中寻找父节点是node.left的节点,进行树的再次拼接。
在剩余的父子关系集合treeList中寻找父节点是node.right的节点,进行树的再次拼接。
输出符合条件的目录ID。
六、JAVA算法源码
public class OdTest04 {
static Node rootNode = null;
static int removeValue = 0;
// 剩余的目录ID
static StringBuilder builder = new StringBuilder();
public static void mAIn(String[] args) {
Scanner sc = new Scanner(System.in);
// 父子关系表的长度m
int m = Integer.valueOf(sc.nextLine());
// m个父子关系
List<int[]> treeList = new ArrayList<>();
for (int i = 0; i < m; i++) {
int[] treeArr = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
if(treeArr[1] == 0){
rootNode = new Node(treeArr[0]);
// 拼接二叉树根ID
builder.Append(treeArr[0]).append(" ");
continue;
}
treeList.add(treeArr);
}
// 待删除的ID
removeValue = Integer.valueOf(sc.nextLine());
/**
* 遍历m个父子关系,拼接成二叉树,拼接剩余的目录ID
*/
dfs(treeList,rootNode);
builder.deleteCharAt(builder.length() - 1);
// 输出符合条件的目录ID
System.out.println(builder);
}
/**
* 深度优先搜索dfs
* @param treeList
* @param node
*/
private static void dfs(List<int[]> treeList, Node node){
/**
* 如果剩余的父子关系集合treeList为0,则不需要再进行dfs
* 如果要dfs的node节点是null,则不需要再寻找其左右子节点
*/
if(treeList.size() == 0 || node == null){
return;
}
for (int i = 0; i < treeList.size(); i++) {
// 父子关系
int[] treeArr = treeList.get(i);
// 如果该关系的父节点是value
if(treeArr[1] == node.value){
// 如果该父节点不是待移除的ID
if(removeValue != node.value) {
int sonValue = treeArr[0];
// 如果该子节点不是待移除的ID
if(removeValue != sonValue){
// 拼接成二叉树
if(node.left == null){
node.left = new Node(sonValue);
}else if(node.right == null){
node.right = new Node(sonValue);
}
// 拼接剩余的目录ID
builder.append(sonValue).append(" ");
}
}
// 移除满足条件的父子关系
treeList.remove(treeArr);
// 父子关系集合treeList移除某节点,treeList长度-1,下一个坐标i也应该-1
i--;
}
}
// 在剩余的父子关系集合treeList中寻找父节点是node.left的节点,进行树的再次拼接
dfs(treeList,node.left);
// 在剩余的父子关系集合treeList中寻找父节点是node.right的节点,进行树的再次拼接
dfs(treeList,node.right);
}
}
七、效果展示
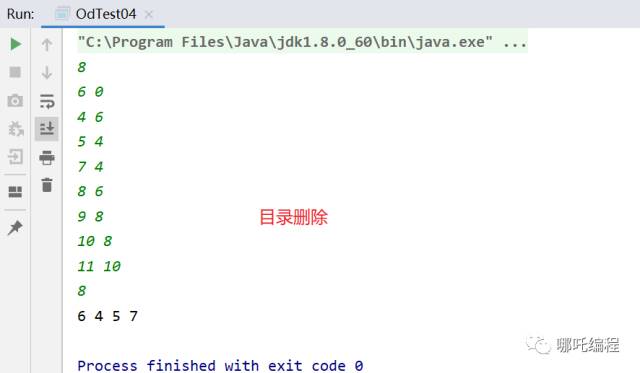
1、输入
8
6 0
4 6
5 4
7 4
8 6
9 8
10 8
11 10
8
2、输出
6 4 5 7
3、说明
输入可以组成二叉树:
6
4 8
5 7 9 10
11
删除值为8的节点,变为6 4 5 7。
4、也许很多人会问,如果节点的值相等,怎么办?
8
6 0
4 6
5 4
5 4
5 6
5 5
10 5
11 10
5
5、输出
6 4
6、说明
输入可以组成二叉树:
6
4 5
5 5 5 10
11
删掉值为5的节点,变为6 4。