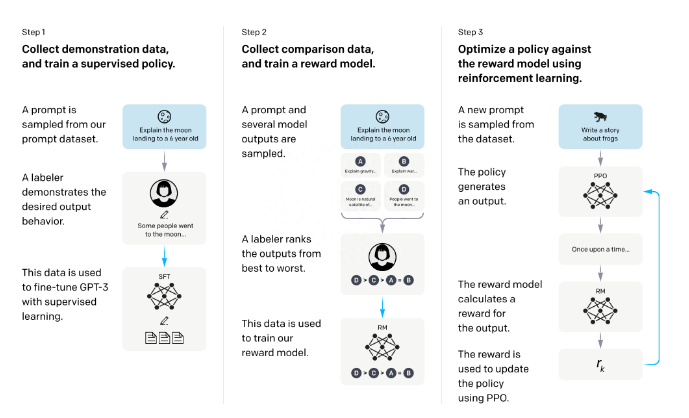
8个核心回归算法总结!!
-
线性回归 -
多项式回归 -
岭回归 -
Lasso回归 -
弹性网络回归 -
逻辑斯蒂回归 -
决策树回归 -
随机森林回归
线性回归(Linear Regression)
-
是预测的目标变量。 -
是输入特征。 -
是斜率(简单线性回归中)或权重(多元线性回归中)。 -
是截距。 -
是多元线性回归中的权重。
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 生成随机数据
np.random.seed(0)
X = np.random.rand(100, 1) # 输入特征
y = 2 * X + 1 + 0.1 * np.random.randn(100, 1) # 生成输出数据,带有一些噪声
# 创建线性回归模型
model = LinearRegression()
# 拟合模型
model.fit(X, y)
# 预测
y_pred = model.predict(X)
# 绘制原始数据和拟合直线
plt.scatter(X, y, label='Original Data')
plt.plot(X, y_pred, color='red', linewidth=3, label='Fitted Line')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title('Linear Regression Example')
plt.show()
LinearRegression模型拟合数据,并绘制了原始数据和拟合直线的可视化图表。
多项式回归(Polynomial Regression)
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
# 生成随机数据
np.random.seed(0)
X = np.sort(5 * np.random.rand(80, 1), axis=0)
y = np.cos(X).ravel() + np.random.randn(80) * 0.1
# 使用多项式特征扩展
poly = PolynomialFeatures(degree=4) # 选择多项式的阶数
X_poly = poly.fit_transform(X)
# 创建线性回归模型
model = LinearRegression()
model.fit(X_poly, y)
# 预测
X_test = np.linspace(0, 5, 100)[:, np.newaxis]
X_test_poly = poly.transform(X_test)
y_pred = model.predict(X_test_poly)
# 绘制原始数据和拟合曲线
plt.scatter(X, y, label='Original Data')
plt.plot(X_test, y_pred, label='Polynomial Regression', color='r')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.title('Polynomial Regression Example')
plt.show()

岭回归(Ridge Regression)
-
是因变量(目标变量)的观测值。 -
是模型的参数,其中 是截距, 是自变量的系数。 -
是第 个观测值的第 个自变量的值。 -
是岭回归的超参数,用于控制正则化的强度。
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import trAIn_test_split
# 生成模拟数据集
np.random.seed(0)
n_samples, n_features = 200, 5
X = np.random.randn(n_samples, n_features)
true_coefficients = np.array([4, 2, 0, 0, -1])
y = X.dot(true_coefficients) + np.random.randn(n_samples) * 1.0
# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 使用岭回归拟合数据
alpha = 1.0 # 正则化强度参数
ridge = Ridge(alpha=alpha)
ridge.fit(X_train, y_train)
# 输出岭回归模型的系数
print("Ridge Regression Coefficients:", ridge.coef_)
# 计算模型在测试集上的R^2分数
r_squared = ridge.score(X_test, y_test)
print("R-squared:", r_squared)
# 绘制实际值和预测值的散点图
plt.scatter(y_test, ridge.predict(X_test))
plt.xlabel("Actual Values")
plt.ylabel("Predicted Values")
plt.title("Ridge Regression: Actual vs. Predicted")
plt.show()

Lasso回归(Lasso Regression)
-
是样本数 -
是观测到的目标值 -
是模型预测的目标值 -
是特征的数量 -
是特征 的系数 -
是正则化参数,控制着正则化的强度。较大的 值将导致更多的特征系数为零。
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# 生成合成数据集
X, y = make_regression(n_samples=100, n_features=2, noise=0.5, random_state=42)
# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建Lasso回归模型
alpha = 1.0 # 正则化参数
lasso = Lasso(alpha=alpha)
# 拟合模型
lasso.fit(X_train, y_train)
# 预测测试集
y_pred = lasso.predict(X_test)
# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse:.2f}")
# 绘制特征系数
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.scatter(X[:, 0], y, label='Feature 1')
plt.scatter(X[:, 1], y, label='Feature 2')
plt.xlabel('Features')
plt.ylabel('Target')
plt.title('Original Data')
plt.legend()
plt.subplot(1, 2, 2)
plt.bar(['Feature 1', 'Feature 2'], lasso.coef_)
plt.xlabel('Features')
plt.ylabel('Coefficient Value')
plt.title('Lasso Coefficients')
plt.show()
Lasso回归对合成数据集进行建模,并且展示了特征系数的可视化。
Lasso回归进行特征选择和建模。弹性网络回归(Elastic.NET Regression)
L1正则化(Lasso正则化)和L2正则化(Ridge正则化)的特性,以解决特征选择和过拟合问题。L1和L2正则化项的组合。-
是均方误差,用来衡量模型预测值与实际值之间的差距。 -
λ()是正则化参数,用于控制正则化的强度。 -
是L1正则化的项,它是模型系数的绝对值之和。 -
是L2正则化的项,它是模型系数的平方和。 -
α()是一个介于0和1之间的参数,用于权衡 L1和L2正则化的贡献。当α时,模型等同于Ridge回归,当α时,模型等同于Lasso回归。
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNet
from sklearn.datasets import make_regression
# 生成示例数据集
X, y = make_regression(n_samples=100, n_features=1, noise=10, random_state=42)
# 创建弹性网络回归模型
elastic_net = ElasticNet(alpha=0.5, l1_ratio=0.5, random_state=42)
# 拟合模型
elastic_net.fit(X, y)
# 预测
y_pred = elastic_net.predict(X)
# 绘制原始数据和拟合线
plt.scatter(X, y, label='Actual Data', color='b')
plt.plot(X, y_pred, label='Elastic Net Regression', color='r')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title('Elastic Net Regression')
plt.show()
# 打印模型系数
print("Elastic Net Coefficients:")
print("Intercept:", elastic_net.intercept_)
print("Coefficient:", elastic_net.coef_)

Intercept: 0.05906898426354079
Coefficient: [33.78639071]
逻辑斯蒂回归(Logistic Regression)
-
是观测到类别1的概率。 -
是输入特征向量。 -
是特征权重向量。 -
是偏置项。 -
是自然对数的底数。
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix
from sklearn.preprocessing import StandardScaler
# 生成模拟数据
X, y = make_classification(n_samples=1000, n_features=2, n_classes=2, n_clusters_per_class=1, n_redundant=0, random_state=42)
# 数据标准化
scaler = StandardScaler()
X = scaler.fit_transform(X)
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 训练逻辑斯蒂回归模型
model = LogisticRegression()
model.fit(X_train, y_train)
# 预测
y_pred = model.predict(X_test)
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')
# 绘制决策边界和数据点
xx, yy = np.meshgrid(np.linspace(X[:, 0].min() - 1, X[:, 0].max() + 1, 100),
np.linspace(X[:, 1].min() - 1, X[:, 1].max() + 1, 100))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.RdBu, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.RdBu, marker='o')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Logistic Regression Decision Boundary')
plt.show()

决策树回归(Decision Tree Regression)
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
# 创建一个模拟数据集
np.random.seed(0)
X = np.sort(5 * np.random.rand(80, 1), axis=0)
y = np.sin(X).ravel() + np.random.normal(0, 0.1, X.shape[0])
# 训练决策树回归模型
regressor = DecisionTreeRegressor(max_depth=5)
regressor.fit(X, y)
# 生成预测结果
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_pred = regressor.predict(X_test)
# 绘制原始数据和决策树回归结果
plt.figure()
plt.scatter(X, y, s=20, edgecolor="black", c="darkorange", label="data")
plt.plot(X_test, y_pred, color="cornflowerblue", linewidth=2, label="prediction")
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()

随机森林回归(Random Forest Regression)
-
随机性:随机森林采用随机抽样技术,从训练数据中随机选择样本,并在每个决策树的节点上随机选择特征,以降低过拟合的风险。
-
集成:多个决策树的预测结果被组合,通常采用平均值(对于回归问题)或投票(对于分类问题)来生成最终的预测结果,这有助于降低模型的方差。
-
特征选择:在构建每个决策树时,随机森林只考虑特征的随机子集,从而增加了模型的多样性。
-
鲁棒性:由于随机森林由多个决策树组成,它对于噪声和异常值的鲁棒性较高,可以提供更稳定的预测。
-
是随机森林中的决策树数量。 -
是第 个决策树的预测值。
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error
# 创建一个示例数据集
np.random.seed(0)
X = np.sort(5 * np.random.rand(80, 1), axis=0)
y = np.sin(X).ravel() + np.random.rand(80)
# 创建随机森林回归模型
rf_regressor = RandomForestRegressor(n_estimators=100, random_state=42)
# 训练模型
rf_regressor.fit(X, y)
# 预测
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_pred = rf_regressor.predict(X_test)
# 计算均方误差
mse = mean_squared_error(y, rf_regressor.predict(X))
print("Mean Squared Error:", mse)
# 绘制真实值和预测值的可视化图表
plt.figure(figsize=(10, 6))
plt.scatter(X, y, s=20, edgecolor="black", c="darkorange", label="data")
plt.plot(X_test, y_pred, color="cornflowerblue", linewidth=2, label="prediction")
plt.xlabel("data")
plt.ylabel("target")
plt.title("Random Forest Regression")
plt.legend()
plt.show()