算法算法
从1950年代的早期研究开始,机器学习的所有工作似乎都随着神经网络的创建而积累起来。 从逻辑回归到支持向量机,相继提出了新算法之后的算法,但是从字面上看,神经网络是算法算法和机器学习的顶峰。 它是什么是机器学习的普遍概括,而不是一种尝试。
从这个意义上讲,它不仅仅是一个算法,而不仅仅是一个框架和一个概念,考虑到构建神经网络的大量自由性,这是显而易见的-隐藏层和节点数,激活函数,优化器,损失函数,网络类型( 卷积,递归等)和专用层(批处理规范,辍学等),仅举几例。
从这个角度来看,神经网络是一个概念,而不是一个严格的算法,这带来了一个非常有趣的推论:任何机器学习算法,无论是决策树还是k近邻,都可以使用神经网络来表示。 虽然本能地通过几个示例可以理解,但是该陈述可以在数学上得到证明。
首先让我们定义一个神经网络:它是一个由输入层,隐藏层和输出层组成的体系结构,每一层的节点之间都有连接。 信息通过线性变换(权重和偏差)从非线性层(激活函数)从输入层转换为输出层。 有一些方法可以更新模型的可训练参数,例如…
Logistic回归简单定义为标准回归,每个输入均具有乘法系数,并添加了附加截距,所有截距均通过S型函数传递。 这可以通过没有隐藏层的神经网络来建模。 结果是通过S形输出神经元的多元回归。
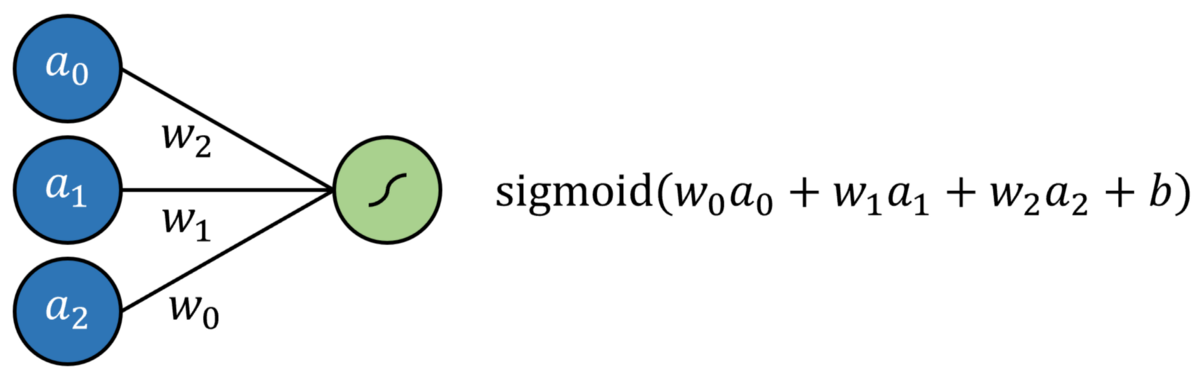
通过将输出神经元激活函数替换为线性激活函数(可以简单地映射输出f(x)= x,换句话说,它什么都不做),可以对线性回归进行建模。
支持向量机(SVM)算法尝试通过所谓的"内核技巧"将数据投影到新空间中,从而优化数据的线性可分离性。 转换完数据后,该算法将绘制最能沿类边界将数据分开的超平面。 超平面被简单地定义为现有维度的线性组合,非常像2维的直线和3维的平面。从这个意义上讲,人们可以将SVM算法看作是数据到新空间的投影,然后是 多重回归。 神经网络的输出可以通过某种有界输出函数传递,以实现概率结果。

当然,可能需要实施一些限制,例如限制节点之间的连接并固定某些参数,这些更改当然不会脱离"神经网络"标签的完整性。 也许需要添加更多的层,以确保支持向量机的这种表现能够达到与实际交易一样的效果。
诸如决策树算法之类的基于树的算法有些棘手。 关于如何构建这种神经网络的答案在于分析它如何划分其特征空间。 当训练点遍历一系列拆分节点时,特征空间将拆分为多个超立方体。 在二维示例中,垂直线和水平线创建了正方形。

> Source: DataCamp community. Image free to share.
因此,可以通过更严格的激活来模拟沿特征线分割特征空间的类似方式,例如阶跃函数,其中输入是一个值或另一个值-本质上是分隔线。 权重和偏差可能需要实施值限制,因此仅用于通过拉伸,收缩和定位来定向分隔线。 为了获得概率结果,可以通过激活函数传递结果。
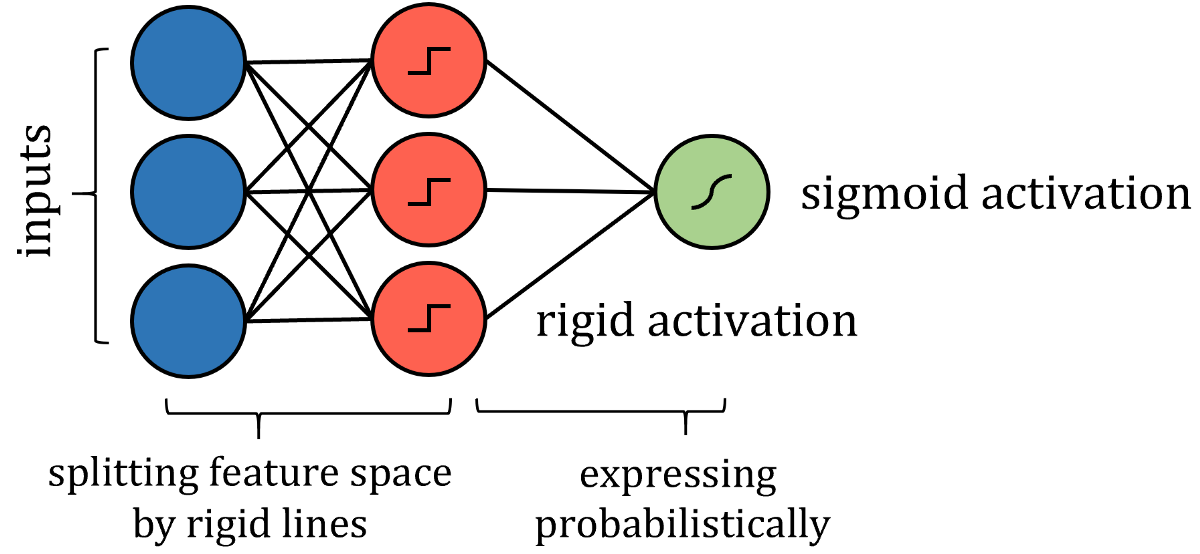
尽管算法的神经网络表示与实际算法之间存在许多技术差异,但重点是网络表达的思想相同,并且可以以与实际算法相同的策略和性能来解决问题。
但是,也许您不满意将算法粗略地转换为神经网络形式,或者希望看到通用的应用程序甚至更棘手的算法,例如k近邻算法或朴素贝叶斯算法,而不是逐案解决。 答案就在于普遍近似定理-神经网络大获成功的数学解释-本质上说,足够大的神经网络可以以任意精度对任何函数建模。 假设有一些函数f(x)代表数据; 对于每个数据点(x,y),f(x)始终返回等于或非常接近y的值。

建模的目的是找到该代表性或真理函数f(x),我们将其表示为预测的p(x)。 所有机器学习算法对这个任务的处理方式都大不相同,将不同的假设视为有效,并给出其最佳结果p(x)。 如果要写出算法创建p(x)的方式,您可能会从条件列表到纯粹的数学运算中得到任何东西。 描述函数如何将目标映射到输入的函数实际上可以采用任何形式。

有时,这些功能起作用。 在其他时候,它们却没有—它们具有固定数量的参数,使用或保留它是一件重要的事情。 但是,神经网络在寻找f(x)的方式上有些不同。
任何函数都可以由许多类似阶梯的部分合理地逼近-步数越多,逼近的精度就越高。

这些步骤中的每一个都在神经网络中表示,即隐层中具有S型激活函数的节点,该函数本质上是概率阶跃函数。 本质上,每个节点都"分配"给函数f(x)的一部分。 然后,通过权重和偏差系统,网络可以确定节点的存在,如果需要为特定输入激活神经元,则将S型函数的输入向无穷大(输出为1),否则向负无穷大。 。 不仅在数值数据中而且在图像中也观察到了这种委托节点以寻找数据功能的特定部分的模式。
尽管通用逼近定理已扩展为适用于其他激活函数(如ReLU和神经网络类型),但原理仍然适用:神经网络的创建是完美的。 神经网络不再依赖于复杂的方程和关系数学系统,而是将自身的一部分委派给数据功能的一部分,并通过蛮力记忆将其归纳在其指定区域内。 当这些节点被聚集到一个庞大的神经网络中时,当它们实际上是巧妙设计的近似器时,结果是一个看似智能的模型。
假设神经网络至少可以在理论上构造出一个函数,该函数基本上具有所需的精度(节点数越多,近似值越准确,当然不考虑过拟合的技术性),具有正确结构的神经网络可以 对任何其他算法的预测函数p(x)建模。 关于其他任何机器学习算法,都不能这么说。
神经网络使用的方法不是优化现有模型中的一些参数,例如多项式曲线或节点系统。 神经网络是对数据建模的某种观点,其目的不是要充分利用任何独立系统,而是要直接逼近数据功能。 我们非常熟悉的神经网络架构仅仅是一个真正想法的模型体现。
借助神经网络的力量以及对深度学习的无底领域的不断研究,无论是视频,声音,流行病学数据还是两者之间的任何数据,都将能够以前所未有的程度建模。 神经网络确实是算法的算法。
除非另有说明,否则所有图片均由作者创建。
(本文翻译自Matthew P. Burruss的文章《Every machine Learning Algorithm Can Be Represented as a Neural Network》,参考:https://towardsdatascience.com/every-machine-learning-algorithm-can-be-represented-as-a-neural-network-82dcdfb627e3)