作者 | Mr Bear
编辑 | 丛 末
近年来,随着图神经网络在各个领域的火热应用,越来越多的学者试图从图论的角度对图神经网络的表达能力进行理论分析,并基于这些理论分析开发出了性能强大的模型。然而,在实际应用中,这些在理论上非常强大的模型的性能往往会受到计算复杂度等因素的限制。
本文作者 Michael Bronstein 是一名来 自帝国理工学院的教授,同时也是 Twitter 图机器学习项目组的负责人。在本文中,他深入浅出地介绍了近年来分析图神经网络表达能力的工作,并介绍了他们对于该领域未来发展方向的思考。
1图神经网络和 WL 图同构测试之间的关系
众所周知,传统的前馈神经网络(多层感知机)是一种通用函数近似器:它们能够以任意的准确率逼近任意的平滑函数。对于近期兴起的图神经网络来说,其表征性质还不太为人所知。在实验中,我们经常可以看到图神经网络在某些数据集上性能优异,但同时又在另一些数据集上表现令人失望。
为了探究造成这种现象的根本原因,我们不得不思考一个问题:图神经网络究竟有多强大?
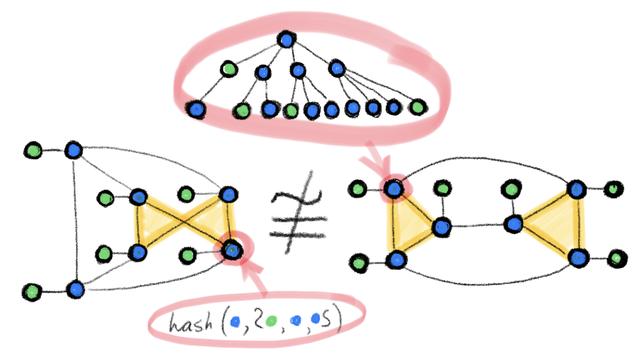
在探究这一问题的过程中,我们所面临的一个挑战是:实际应用场景下使用的图往往是连续结构和离散结构(节点、边特征、连通性)的组合。因此,该问题可以被表述为不同的形式。一种可能的形式化定义是:图神经网络是否能够区分不同类型的图结构。在图论中,这是一种被称为「图同构问题」的经典问题,旨在判断两个图在拓扑意义上是否等价。两个同构的图拥有相同的连通性,其差别仅仅可能是节点的排列不同。
稍令人惊讶的是,我们尚不知晓精确的图同构问题的复杂度级别。该问题在多项式时间内不可解,它也不是一个 NP 完全(NPC)问题。有时,我们将其复杂度称为一种特殊的「GI 级」(GI class)。
1、Weisfeiler-Lehman 测试
Boris Weisfeiler 和 Andrey Lehman 于 1968 年发表的具有开创性意义的论文「The reduction of a graph to canonical form and the algebra which Appears therein 」),提出了一种高效的启发式算法,我们现在将其称为「WL 测试」。
最初,人们认为 WL 测试可以在多项式时间内求解图同构问题。但一年之后,人们就举出了一个反例。然而,从概率意义上说,似乎 WL 测试对于几乎所有的图都有效。
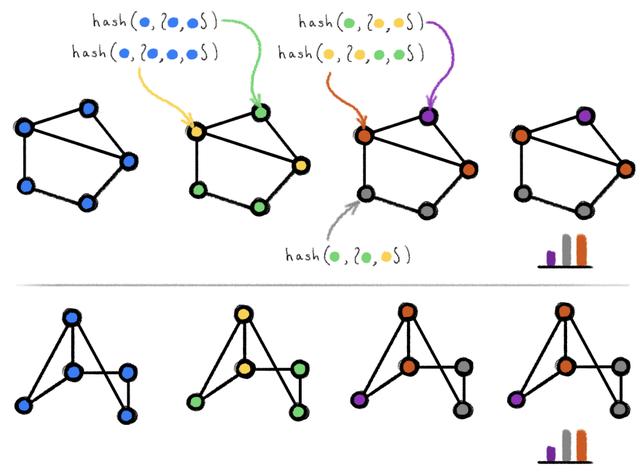
图 1:在两个同构图上执行 WL 测试的示例。包含弧线的 hash 圆括号代表多重集。在着色情况不再变化后算法会终止,并给出输出结果(颜色直方图)。若将两图输入给该算法得到的输出相同,则说明两图可能同构。
WL 测试是建立在迭代式的图重着色(图论中的「着色」指的是一种离散的节点标签)基础上的,在初始状态下,每个节点的颜色均不相同。在每一步迭代中,算法会聚合节点及其邻居节点的颜色,并将它们表征为多重集,然后将聚合得到的颜色多重集通过 Hash 函数映射到某种唯一的新颜色上。当达到稳定的着色状态(各节点着色状态不再变化)后,算法终止。当算法终止后,若两图的着色情况不同,则我们认为它们「非同构」。如果两图着色情况相同,它们可能(但并不一定)是同构的。换句话说,WL 测试是图同构的必要非充分条件。有一些非同构的图在接受 WL 测试后得到的着色情况也是相同的,而在这种情况下 WL 测试就失效了,因此我们只能认为它们「可能同构」。下图展示了其中的一种可能性:
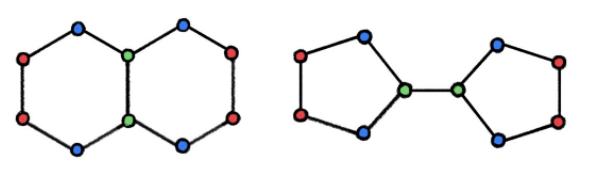
图 2:显然,WL 图同构测试会为上面的两个非同构图生成相同的着色结果,此时 WL 测试失效。在化学领域中,这两个图分别代表两种不同的化合物「decalin」(左图)和「bicyclopentyl」(右图)的分子结构。
2、图同构网络(GIN)
Keyulu Xu 等人发表的论文「 How powerful are graph neural networks?」和 Christopher Morris 等人发表的论文,以及 Thomas 在他至少两年前撰写的博客「GRAPH CONVOLUTIONAL NETWORKS」,中注意到,WL 测试与图消息传递神经网络有惊人的相似之处,它们都在图上进行了一种类似于卷积的操作。
相关论文/文章链接:
https://arxiv.org/abs/1810.00826
https://tkipf.github.io/graph-convolutional-networks/
在一个消息传递层中,每个节点的特征会以聚合其邻居节点特征的方式被更新。对聚合和更新操作的选择是十分重要的:只有使用多重集的单射函数才能使其与 WL 算法等价。在前人的研究中,「取最最大值」或「取均值」等聚合操作都是一定弱于 WL 的能力,它们甚至不能区分非常简单的图结构:
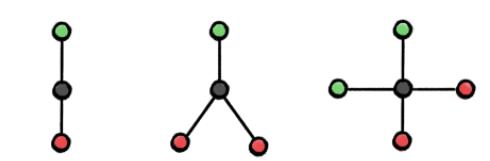
图 3:通过「取最大值」操作无法区分左图、中图、右图,通过「取均值」聚合函数可以区分左图和中图、通过「取最大值」和「取均值」操作均无法区分左图和右图。这是因为通过这些方法从黑色节点的邻居中聚合而来的特征将会是相同的。
Xu 提出了一种聚合和更新函数的选择方案,它使得消息传递神经网络与 WL 算法等价,该网络被称为「图同构网络」(GIN)。该网络和标准的消息传递神经网络一样强大。但是,GIN 不仅仅是一种新的网络架构,其主要影响在于它通过一种简单的设定形式化定义了图神经网络表达能力的问题,这种设定与图论中的经典问题相关。该网络的思路也启发了许多后续的工作。
3、Weisfeiler-Lehman 层次结构
使用更加强大的图同构测试,是扩展 Xu 和 Morris 等人工作的一个方向。因此,László Babai 提出了 k-WL 测试,这是 WL 算法在高阶上的扩展,它在 k 元组上进行操作,而非操作单个节点。除了 1-WL 和 2-WL 测试是等价的,(k+1)-WL 始终严格强于 k-WL(k≥2),即对于某些图而言 k-WL 测试失效,而 (k+1)-WL 测试可以成功判定图是否同构,但反之则不然。因此,k-WL 是一种层次结构的或随着 k 的增大而逐渐更加强大的图同构测试,有时被称为「Weisfeiler-Lehman 层次结构」。
我们可以设计出遵循 k-WL 测试的图神经网络,这种网络是一定比消息传递架构更加强大的。Morris 等人在论文「 Weisfeiler and Leman go neural: Higher-order graph neural networks 」中提出了第一种这样的架构 k-GNN。
相关论文链接:
https://aaai.org/ojs/index.php/AAAI/article/view/4384/4262
传统的消息传递神经网络和这种高阶图神经网络之间最关键的区别在于:由于 k-WL 算法在节点的 k 元组上进行操作,所以这种高阶图神经网络是非局部的(non-local)。这对算法的实现及其计算复杂度和存储复杂度都有重要的影响:k-GNN 需要