一个强大的算法模型：SGD！！

2023-09-15 机器学习和人工智能AI

加入收藏

大家好，今天聊聊随机梯度下降（SGD）

随机梯度下降（Stochastic Gradient Descent，简称SGD）是机器学习和深度学习中的一个重要优化算法。

今天尽力以最简单的方式解释，帮助大家理解。

大白话解释

SGD是一种用于训练机器学习模型的方法，特别是神经网络。

它的目标是找到使我们的模型在给定数据上表现得尽可能好的参数值。

想象一下，你要教一个机器学习模型来识别猫和狗的图片。初始时，模型并不知道如何识别猫和狗。SGD的任务就是通过不断调整模型参数，使它的预测结果更接近实际情况。

基本原理

SGD的基本原理非常简单。它通过以下步骤进行工作：

初始化参数：首先，我们随机初始化模型的参数，就像开始时我们不知道任何关于猫和狗的信息。
选择一个样本：然后，从我们的数据集中随机选择一个样本（一张猫或狗的图片）。
计算梯度：用选定的样本来计算模型的梯度，这告诉我们如何调整参数以减小预测误差。
更新参数：接下来，我们使用梯度信息来微调参数，以使模型更好地预测选定的样本。
重复：然后，我们重复这个过程，不断选择不同的样本并更新参数，直到我们认为模型已经足够好地理解了数据。

详细的公式解释

SGD的核心数学公式如下：

θ' = θ - α * ∇J(θ, xi, yi)

θ是模型的参数。
α是学习率，它决定了参数更新的步长。
∇J(θ, xi, yi)是损失函数关于参数θ的梯度，它告诉我们如何调整参数以减小损失函数J(θ, xi, yi)。xi和yi是选定的训练样本。

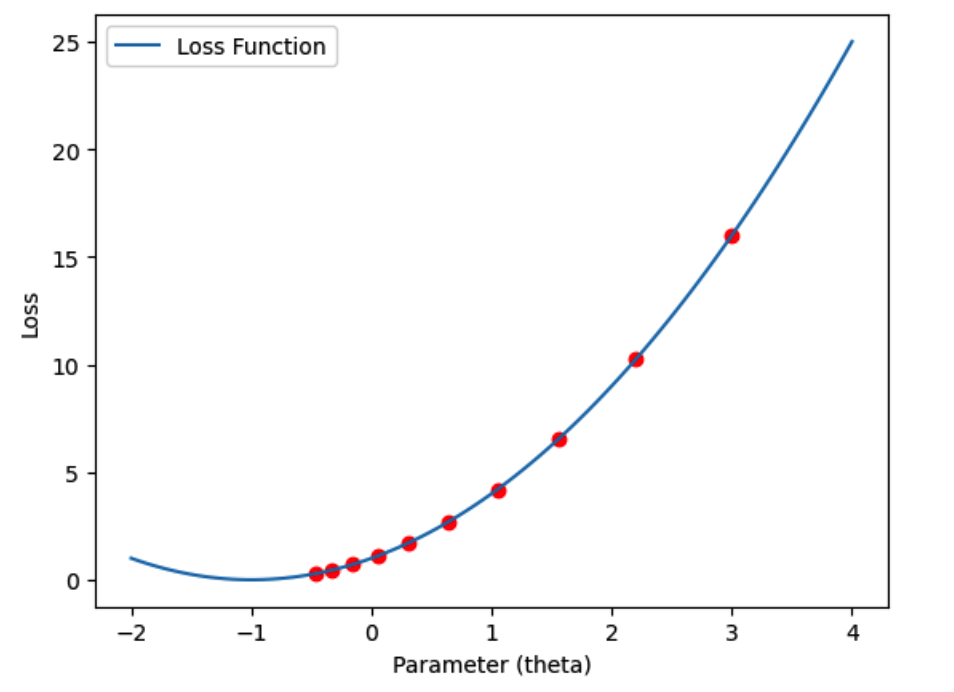
利用Python/ target=_blank class=infotextkey>Python绘制示意图

让我们使用Python来绘制一个简单的示意图，以帮助你更好地理解SGD的工作原理。首先，确保你已经安装了Matplotlib库，然后可以使用以下代码：

import matplotlib.pyplot as plt
import numpy as np

# 模拟一个简单的损失函数
def loss_function(theta):
    return theta**2 + 2*theta + 1

# 损失函数的梯度
def gradient(theta):
    return 2*theta + 2

# 初始化参数和学习率
theta = 3.0
learning_rate = 0.1
iterations = 10

# 绘制损失函数和参数更新过程
losses = []

for i in range(iterations):
    loss = loss_function(theta)
    losses.Append(loss)
    plt.plot(theta, loss, 'ro')  # 绘制当前参数和损失值
    gradient_value = gradient(theta)
    theta -= learning_rate * gradient_value  # 更新参数

# 绘制损失函数曲线
theta_values = np.linspace(-2, 4, 100)
loss_values = loss_function(theta_values)
plt.plot(theta_values, loss_values, label='Loss Function')
plt.xlabel('Parameter (theta)')
plt.ylabel('Loss')
plt.legend()
plt.show()

这段代码将绘制一个简单的损失函数曲线，并演示了参数如何随着迭代次数的增加而更新。

一个强大的算法模型：SGD！！

再举一个案例

要可视化随机梯度下降（SGD）的三维工作示例，我们可以创建一个模拟的损失函数，并在不断迭代的过程中更新参数以最小化损失。

这里我将使用Matplotlib来绘制三维图形，并使用大量的数据点来可视化SGD的工作。请注意，这只是一个示例，用于直观演示SGD的工作原理。

如果没有安装matplotlib，可以使用pip：

pip install matplotlib

使用Python代码来创建可视化SGD图像：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 模拟损失函数
def loss_function(x, y):
    return x**2 + y**2

# 模拟梯度计算
def gradient(x, y):
    dx = 2 * x
    dy = 2 * y
    return dx, dy

# 随机梯度下降
def stochastic_gradient_descent(learning_rate, num_iterations):
    history = []

    # 随机初始值
    x, y = np.random.rand(2) * 10

    for _ in range(num_iterations):
        grad_x, grad_y = gradient(x, y)
        x -= learning_rate * grad_x
        y -= learning_rate * grad_y
        history.append((x, y))

    return np.array(history)

# 设置学习率和迭代次数
learning_rate = 0.1
num_iterations = 100

# 运行随机梯度下降
sgd_history = stochastic_gradient_descent(learning_rate, num_iterations)

# 可视化损失函数
x = np.linspace(-10, 10, 100)
y = np.linspace(-10, 10, 100)
X, Y = np.meshgrid(x, y)
Z = loss_function(X, Y)

# 创建3D图形
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# 绘制损失函数表面
ax.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)

# 绘制随机梯度下降路径
sgd_x, sgd_y = zip(*sgd_history)
sgd_z = loss_function(np.array(sgd_x), np.array(sgd_y))
ax.plot(sgd_x, sgd_y, sgd_z, marker='o', color='r', linestyle='-')

# 设置图形属性
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Loss')
ax.set_title('Stochastic Gradient Descent')

plt.show()

这个代码将创建一个三维图形，其中损失函数的表面用虚线表示，并且随机梯度下降的路径用红色线条表示。

一个强大的算法模型：SGD！！

可以根据需要调整学习率和迭代次数，以及损失函数和梯度的定义，以适应不同的示例和问题。