在PyTorch中有四种类型的乘法运算（位置乘法、点积、矩阵与向量乘法、矩阵乘法），非常容易搞混，我们一起来看看这四种乘法运算的区别。

位置乘法

先构建两个张量a，b他们都是4行5列。

a = torch.arange(20).reshape([4,5])
b = torch.randn([4,5])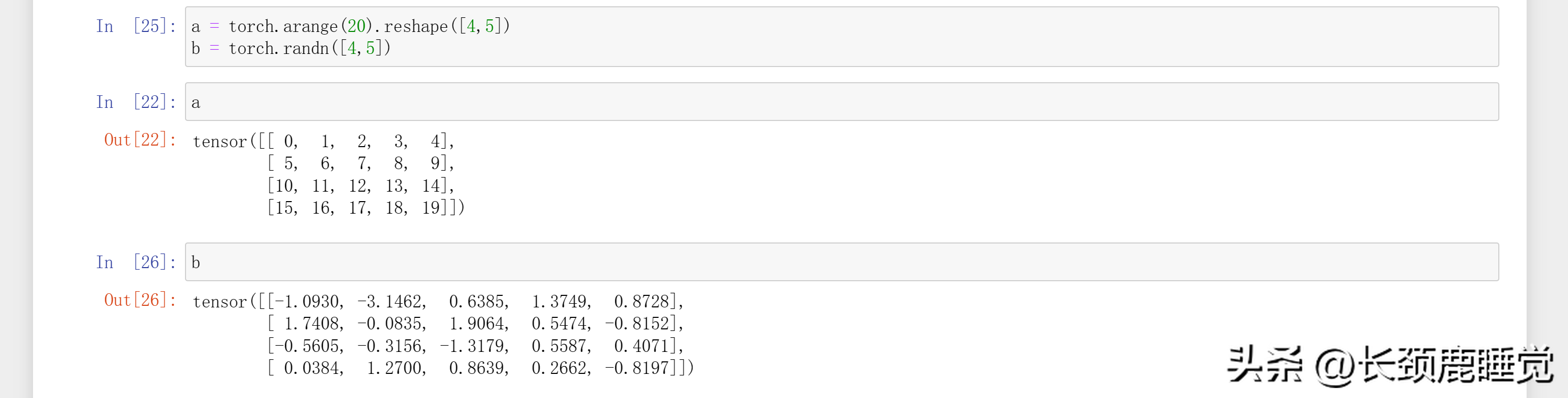

位置乘法，顾名思义就是将两个张量对应位置的元素进行乘法运算，运算符是*。

可以是两个张量相乘，也可以是标量和张量相乘。

标量与张量相乘，是用标量与张量的每个元素相乘，结果张量的形状不变。

4 * a

两个张量相乘，是对应位置的元素相乘，结果张量的形状不变。

a * b

点积

点积是两个向量（也就是一维张量）对应位置的元素相乘后求和，结果是一个标量，使用dot函数进行计算。

先构建两个向量a、b，点积操作要求两个向量的数据类型要一致，因此a中指定数据类型为float。

a = torch.arange(6, dtype=torch.float32)
b = torch.ones(6)

执行点积操作，结果是一个标量。

torch.dot(a,b)

矩阵与向量乘法

矩阵（二维张量）与向量（一维张量）的乘法是将矩阵的每一行与向量进行点积，要求矩阵的列维数与向量的维数相同，结果的维数与行数相同。

使用mv函数进行运算。

构建一个4行5列的矩阵和一个维数为5的向量。

a = torch.arange(20,dtype=torch.float32).reshape([4,5])
b = torch.ones(5)

使用mv函数相乘后，结果是维数为4的向量。

torch.mv(a,b)

矩阵乘法

矩阵（二维张量）乘法是用第一个矩阵的行向量与第二个矩阵的列向量进行点积，要求第一个矩阵的列数与第二个矩阵的行数相同。

使用mm函数进行运算。

构建两个矩阵，一个4行5列，一个5行6列

a = torch.arange(20,dtype=torch.float32).reshape([4,5])
b = torch.randn([5,6])

使用mm函数相乘后，结果是4行6列的矩阵。

torch.mm(a,b)