网页CAD的mxdraw库实现Autocad中的圆
Web端显示CAD图纸的应用场景很广泛,单纯的浏览DWG逐渐满足不了用户的实际需求,浏览的同时再加上简单的绘制和批注更符合大家的应用场景,接下来我们讲一下如何利用Mxdraw库实现AutoCAD中的画圆命令。
首先我们知道DWG图纸要在网页上显示需要安装转换程序,在测试开始之前,我们要熟悉转换方法和原理,请查看快速入门(https://help.mxdraw.com/?pid=32)中的《如何在自己系统中浏览dwg文件》章节,如下图所示:
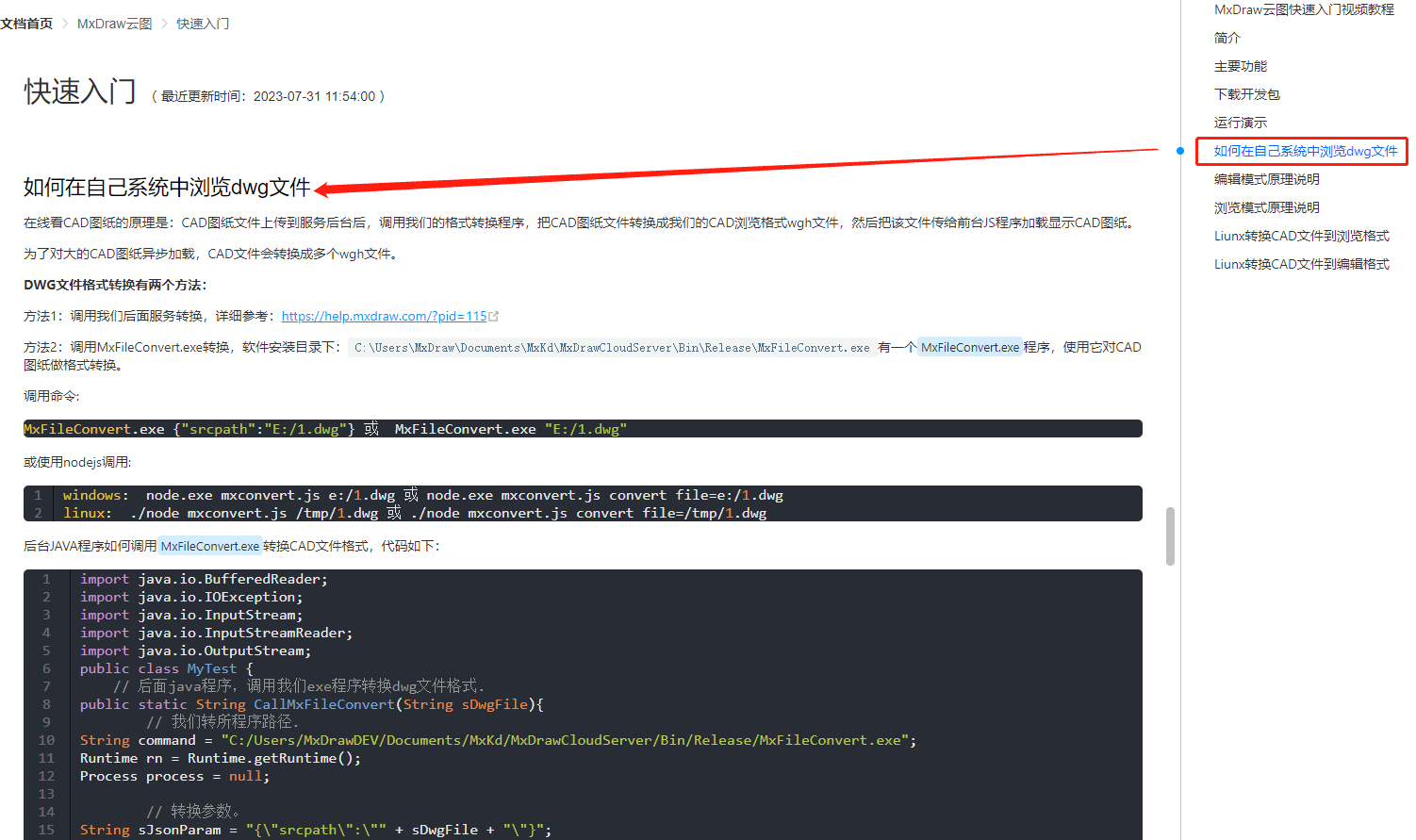
如果还有不清楚的,可以查看:(https://help.mxdraw.com/?pid=107)中《mxdraw前端库预览图纸》章节,如下图:
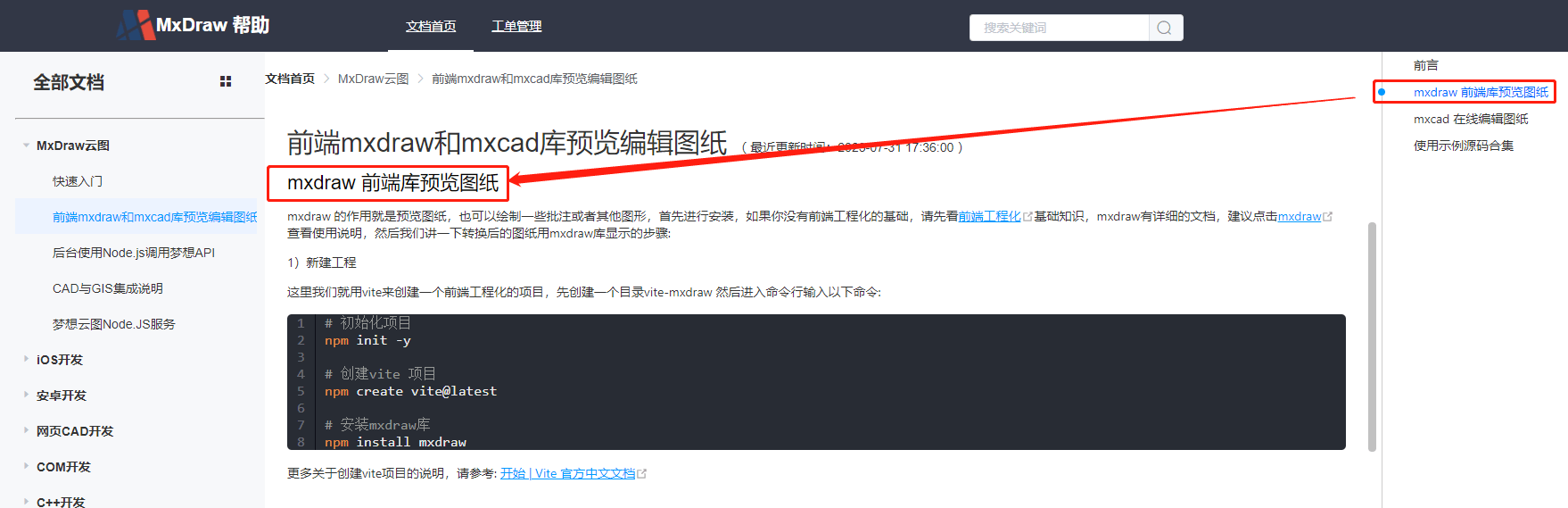
关于[MxDbCircleShape]
mxdraw库是一款用于绘制CAD图形的JAVAScript库,它提供了一系列的图形形状类,可以实现类似于Autocad的绘图功能,在此之前先看一下圆弧形状类的描述:[MxDbCircleShape圆(弧)形状类]https://mxcadx.gitee.io/mxdraw_api_docs/classes/MxDbCircleShape.html。
基于这个形状类, 我们可以实现类似autocad绘制圆的功能,首先我们先通过继承类的方式,为圆提供可以改变这个圆的夹点,代码如下:
import { MxDbCircleShape } from "mxdraw";
class MxDbCircle extends MxDbCircleShape {
/**是否闭合到中心位置 */
isClosedToCenter = false
/**
* 返回自定义对象的夹点.
* @param
* @returns Array<THREE.Vector3>
*/
getGripPoints() {
const { x, y, z } = this.center;
// 计算圆的上下左右夹点
let upPoint = new THREE.Vector3(x, y + this.radius, z),
downPoint = new THREE.Vector3(x, y - this.radius, z),
leftPoint = new THREE.Vector3(x - this.radius, y, z),
rightPoint = new THREE.Vector3(x + this.radius, y, z);
return [this.center, upPoint, downPoint, leftPoint, rightPoint];
}
/**
* 移动自定义对象的夹点.
* @param
* @returns boolean
*/
moveGripPointsAt(index: number, offset: THREE.Vector3) {
const [center, upPoint, downPoint, leftPoint, rightPoint] =
this.getGripPoints();
// 改变上下左右的夹点则改变radius半径
if (index === 0) this.center = center.add(offset);
if (index === 1) this.radius = upPoint.add(offset).distanceTo(this.center);
if (index === 2)
this.radius = downPoint.add(offset).distanceTo(this.center);
if (index === 3)
this.radius = leftPoint.add(offset).distanceTo(this.center);
if (index === 4)
this.radius = rightPoint.add(offset).distanceTo(this.center);
return true;
}
}
属性列表如下:
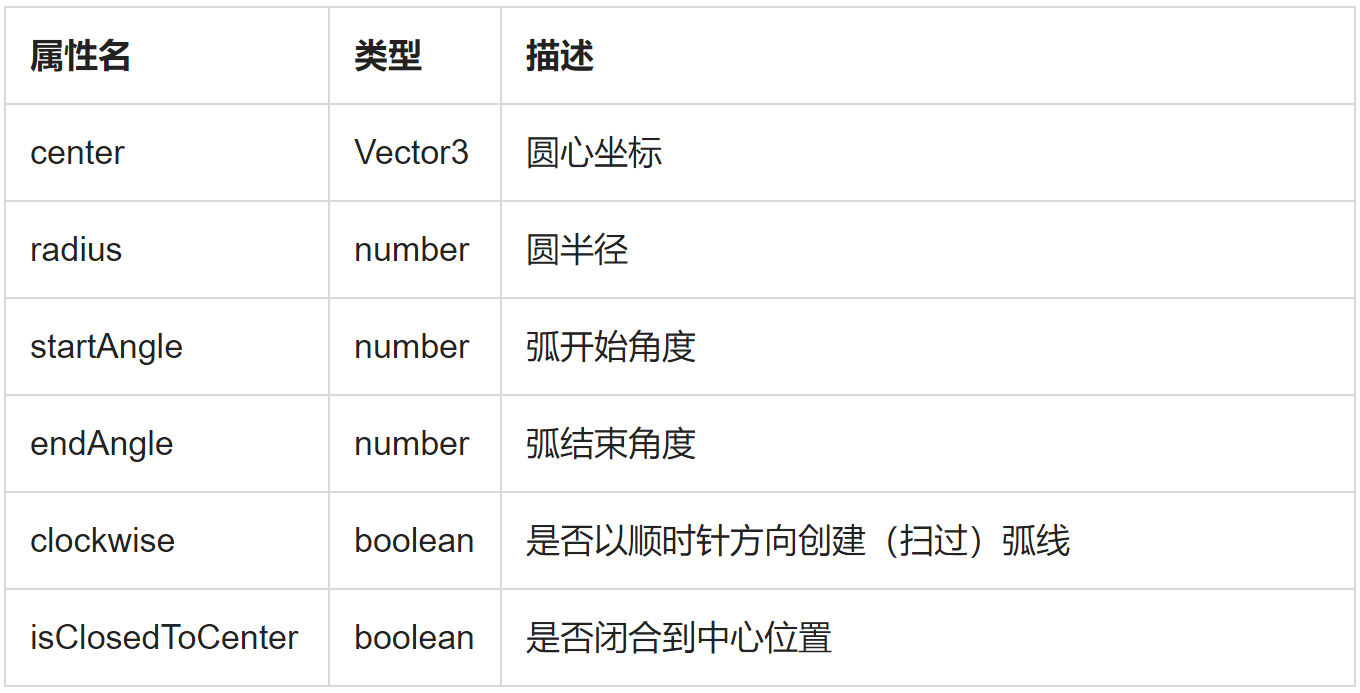
需要注意的是MxDbCircleShape继承自[MxDbEllipseShape](https://mxcadx.gitee.io/mxdraw_api_docs/classes/MxDbEllipseShape.html),因此MxDbCircleShape也拥有MxDbEllipseShape的所有属性。我们只需要知道圆心和半径就可与直接绘制一个圆了,在Autocad中绘制圆的方式有很多种, 下面介绍两种方式来绘制圆:
方法一:两点绘制圆
参考代码如下:
import { MrxDbgUiPrPoint, MxFun, MxDbCircleShape, McEdGetPointWorldDrawObject, } from "mxdraw";
const drawCircleAtTwoPoints = async () => {
const getPoint = new MrxDbgUiPrPoint();
const circle = new MxDbCircle();
// 直接确定圆心
circle.center = awAIt getPoint.go()
getPoint.setUserDraw(
(
currentPoint: THREE.Vector3,
pWorldDraw: McEdGetPointWorldDrawObject
)=> {
// 根据圆心和圆弧上任意一点确定半径
circle.radius = circle.center.distanceTo(currentPoint)
pWorldDraw.drawCustomEntity(circle);
// 再绘制一根圆弧和圆心的连接线表示现在正在确定半径
pWorldDraw.drawLine(circle.center, currentPoint);
}
);
// 确定最后绘制的圆的半径
circle.radius = circle.center.distanceTo(await getPoint.go())
MxFun.getCurrentDraw().addMxEntity(circle);
}
drawCircleAtTwoPoints()
方法二:三点绘制圆
通过三元一次方程组求解圆心的坐标的具体步骤如下:
1)假设圆心的坐标为(cx, cy, cz),将三个点的坐标代入圆的一般方程,得到三个方程:
a1 * cx + b1 * cy + c1 * cz + d1 = 0
a2 * cx + b2 * cy + c2 * cz + d2 = 0
a3 * cx + b3 * cy + c3 * cz + d3 = 0
2)将三个方程进行整理,得到以下形式的方程:
(a1 * b2 * c3 - a1 * b3 * c2 - a2 * b1 * c3 + a2 * b3 * c1 + a3 * b1 * c2 - a3 * b2 * c1) * cx +
(b1 * c2 * d3 - b1 * c3 * d2 - b2 * c1 * d3 + b2 * c3 * d1 + b3 * c1 * d2 - b3 * c2 * d1) * cy +
(a1 * b2 * d3 - a1 * b3 * d2 - a2 * b1 * d3 + a2 * b3 * d1 + a3 * b1 * d2 - a3 * b2 * d1) * cz +
(a1 * b2 * c3 - a1 * b3 * c2 - a2 * b1 * c3 + a2 * b3 * c1 + a3 * b1 * c2 - a3 * b2 * c1) = 0
3)根据方程的系数,将cx、cy和cz的系数分别除以(a1 * b2 * c3 - a1 * b3 * c2 - a2 * b1 * c3 + a2 * b3 * c1 + a3 * b1 * c2 - a3 * b2 * c1),得到cx、cy和cz的值。将得到的cx、cy和cz的值作为圆心的坐标,返回一个新的THREE.Vector3对象。
4)这样就可以通过三元一次方程组的求解方法,求得三个点确定的圆心的坐标,代码如下:
export const threePointsToDeterm.NETheCenterOfTheCircle = (
points: [THREE.Vector3, THREE.Vector3, THREE.Vector3]
) => {
const [point1, point2, point3] = points;
const { x: x1, y: y1, z: z1 } = point1;
const { x: x2, y: y2, z: z2 } = point2;
const { x: x3, y: y3, z: z3 } = point3;
const a1 = y1 * z2 - y2 * z1 - y1 * z3 + y3 * z1 + y2 * z3 - y3 * z2,
b1 = -(x1 * z2 - x2 * z1 - x1 * z3 + x3 * z1 + x2 * z3 - x3 * z2),
c1 = x1 * y2 - x2 * y1 - x1 * y3 + x3 * y1 + x2 * y3 - x3 * y2,
d1 = -(
x1 * y2 * z3 -
x1 * y3 * z2 -
x2 * y1 * z3 +
x2 * y3 * z1 +
x3 * y1 * z2 -
x3 * y2 * z1
),
a2 = 2 * (x2 - x1),
b2 = 2 * (y2 - y1),
c2 = 2 * (z2 - z1),
d2 = x1 * x1 + y1 * y1 + z1 * z1 - x2 * x2 - y2 * y2 - z2 * z2,
a3 = 2 * (x3 - x1),
b3 = 2 * (y3 - y1),
c3 = 2 * (z3 - z1),
d3 = x1 * x1 + y1 * y1 + z1 * z1 - x3 * x3 - y3 * y3 - z3 * z3,
// 计算圆心的坐标
cx =
-(
b1 * c2 * d3 -
b1 * c3 * d2 -
b2 * c1 * d3 +
b2 * c3 * d1 +
b3 * c1 * d2 -
b3 * c2 * d1
) /
(a1 * b2 * c3 -
a1 * b3 * c2 -
a2 * b1 * c3 +
a2 * b3 * c1 +
a3 * b1 * c2 -
a3 * b2 * c1),
cy =
(a1 * c2 * d3 -
a1 * c3 * d2 -
a2 * c1 * d3 +
a2 * c3 * d1 +
a3 * c1 * d2 -
a3 * c2 * d1) /
(a1 * b2 * c3 -
a1 * b3 * c2 -
a2 * b1 * c3 +
a2 * b3 * c1 +
a3 * b1 * c2 -
a3 * b2 * c1),
cz =
-(
a1 * b2 * d3 -
a1 * b3 * d2 -
a2 * b1 * d3 +
a2 * b3 * d1 +
a3 * b1 * d2 -
a3 * b2 * d1
) /
(a1 * b2 * c3 -
a1 * b3 * c2 -
a2 * b1 * c3 +
a2 * b3 * c1 +
a3 * b1 * c2 -
a3 * b2 * c1);
return new THREE.Vector3(cx, cy, cz);
};
5)已经知道通过三个圆上的点计算出圆心的算法,那么我们就可以通过三个点绘制一个圆,代码如下:
import { MrxDbgUiPrPoint, MxFun, McEdGetPointWorldDrawObject, } from "mxdraw"
const drawCircleAtThreePoints = async () => {
const getPoint = new MrxDbgUiPrPoint();
const circle = new MxDbCircle();
let points = [] as unknown as [THREE.Vector3, THREE.Vector3, THREE.Vector3]
points.push(await getPoint.go())
getPoint.setUserDraw((currentPoint, pWorldDraw) => {
pWorldDraw.drawLine(points[0], currentPoint)
})
points.push(await getPoint.go())
getPoint.setUserDraw(
(
currentPoint: THREE.Vector3,
pWorldDraw: McEdGetPointWorldDrawObject
)=> {
circle.center = threePointsToDetermineTheCenterOfTheCircle([points[0], points[1], currentPoint])
circle.radius = circle.center.distanceTo(currentPoint)
pWorldDraw.drawCustomEntity(circle);
}
);
points.push(await getPoint.go())
circle.center = threePointsToDetermineTheCenterOfTheCircle(points);
circle.radius = circle.center.distanceTo(points[0]);
MxFun.getCurrentDraw().addMxEntity(circle);
}
drawCircleAtThreePoints()
效果图如下:
Demo源码:
https://gitee.com/mxcadx/mxdraw-article/tree/master/mxdraw%E5%BA%93%E5%AE%9E%E7%8E%B0autocad%E4%B8%AD%E7%9A%84%E5%9C%86