R语言使用多元AR-GARCH模型衡量市场风险|附代码数据
关于GARCH的研究报告,包括一些图形和统计输出。
本文分析将用于制定管理客户和供应商关系的策略准则
假设:
- 贵公司拥有用于生产和分销聚戊二酸的设施,聚戊二酸是一种用于多个行业的化合物。
- 制造和分销过程的投入包括各种石油产品和天然气。价格波动可能非常不稳定。
- 营运资金管理一直是一个挑战,最近汇率的走势严重影响了资金。
- 您的CFO使用期货和场外交易(OTC)工具对冲价格风险。
董事会感到关切的是,公司已连续第五个季度未能实现盈利预期。股东不高兴。罪魁祸首似乎是商品销售成本的波动。
示例
- 您应该问有哪些能源定价模式的关键业务问题?
- 您可以使用哪种方法来管理波动率?
这里有一些想法。关键业务问题可能是:
- 哪些输入价格和汇率比其他输入价格和汇率更不稳定?何时?
- 价格走势相关吗?
- 在市场压力时期,它们的走势会有多动荡?
- 是否有我们可以部署的套期工具或可以用来减轻定价风险?
管理波动
- 建立输入监视系统,以了解哪些输入会影响运行制造和分销流程的哪些成本。
- 监控价格走势和特征,并按流程衡量对关键营业收入构成部分的影响的严重性。
- 内置价格无法承受预警指标。
在本文中,我们将
- 使用波动率聚类
- 拟合AR-GARCH模型
- 从AR-GARCH模型模拟波动率
- 衡量风险
ARCH模型
我们已经研究了波动性聚类。ARCH模型是对此进行建模的一种方法。
这些模型对于金融时间序列特别有用,因为金融时间序列显示出较大的收益率变动时期以及相对平稳的价格变化的间歇时期。
可以从z(t)标准正态变量和初始标准波动率开始指定AR + ARCH模型σ(t)2 = z(t)2。然后,我们用方差ε(t)=(sigma2)1 / 2z(t)ε的平方来调节这些变量。然后我们首先为每个日期计算t = 1 ... n,
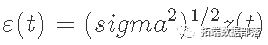
使用该条件误差项,我们计算自回归

现在我们准备计算新的方差项。
n <- 10500
z <- rnorm(n) ## 样本标准正态分布变量
sig2 <- z^2 ##创建波动率序列
omega <- 1 ## 方差
mu <- 0.1 ## 平均收益率
omega/(1-alpha)
sqrt(omega/(1-alpha))
## [1] 2.222222
## [1] 1.490712
for (t in 2:n) ## 滞后于第二个日期开始
{
y[t] <- mu + phi*(y[t-1 -mu) + e[t] ## 收益率
sig2[t+1] <- omega + alpha * e[t ^2 ## 生成新的sigma ^ 2。
结果没有指导意义。
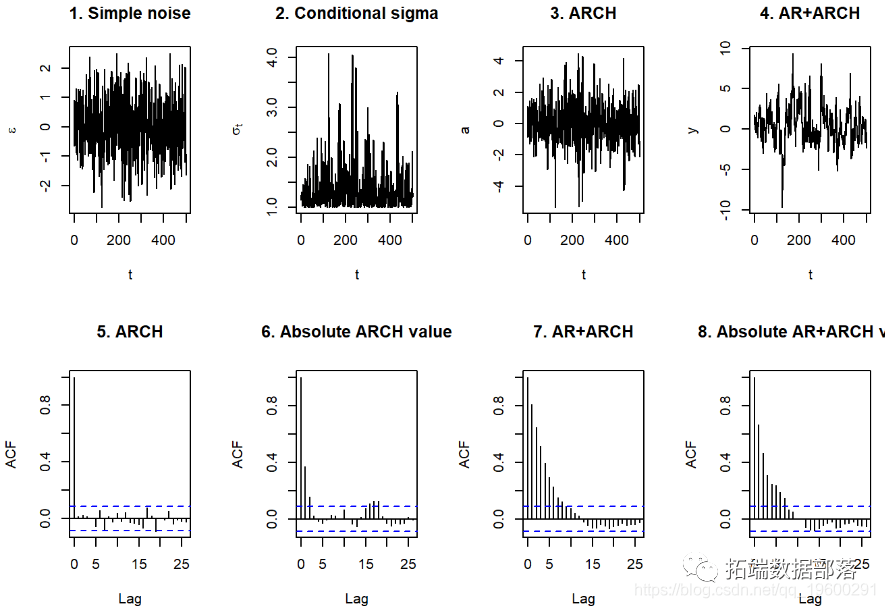
我们可以看到
- 条件标准偏差中较大的孤立峰
- 在ARCH图中也显示
估计
我们有多种方法来估计AR-ARCH过程的参数。首先,让我们加载一些数据。
## 汇率数据是从OANDA获得
data.1 <- na.omit(merge(EUR_USD, GBP_USD,
OIL_Brent))
P <- data.1
R <- na.omit(diff(log(P)) * 100)
然后,我们绘制数据自相关。
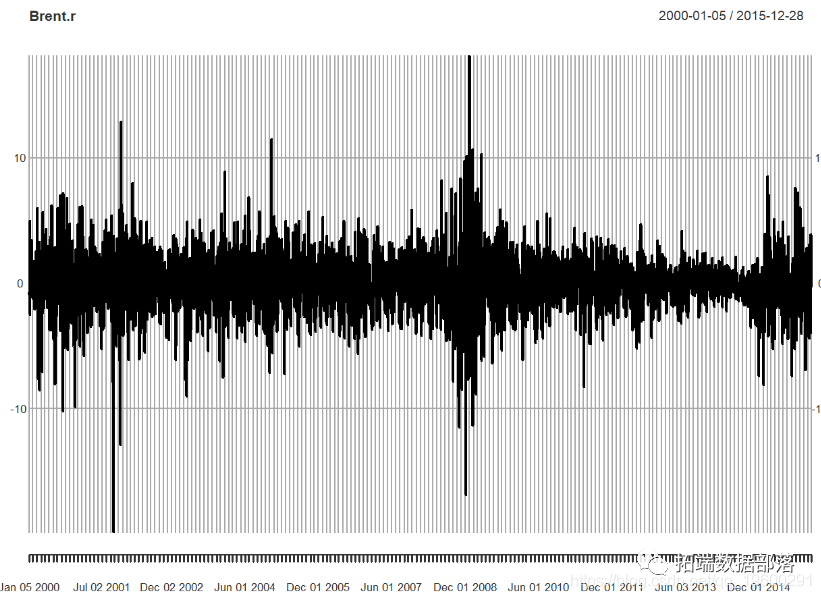
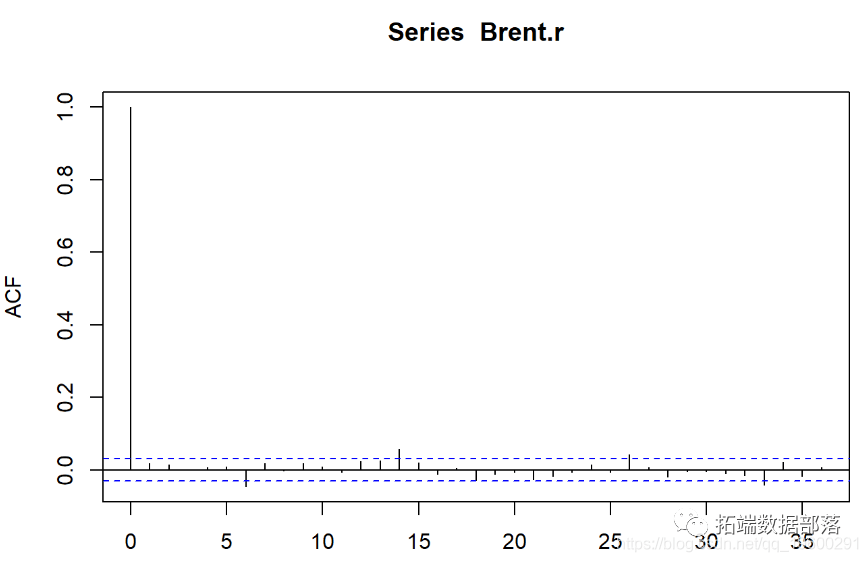
##
## Box-Ljung test
##
## data: Brent.r
## X-squared = 32.272, df = 14, p-value = 0.003664
纯随机性检验,p值小于5%,序列为非白噪声
点击标题查阅往期内容

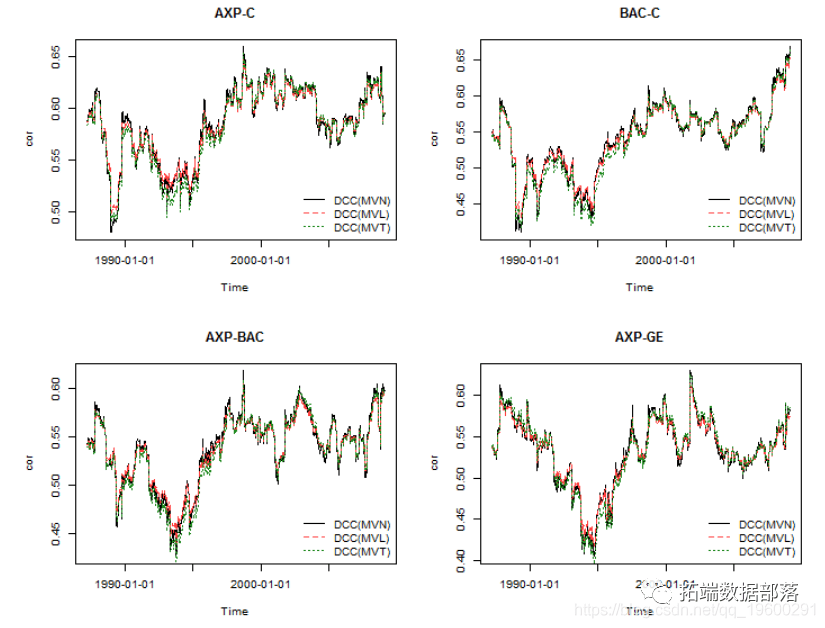
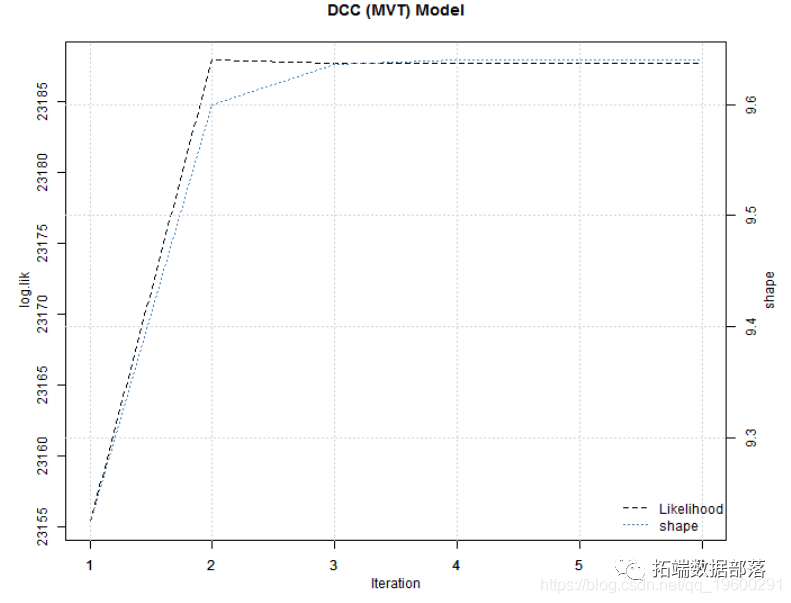
GARCH-DCC模型和DCC(MVT)建模估计

左右滑动查看更多

01
02
03

04

拟合
我们的第一项任务是ARMA-GARCH模型。
- 指定普通sGarch 模型。
- garchOrder = c(1,1) 表示我们使用残差平方和方差的一期滞后:

- 使用 armaOrder = c(1,0) 指定长期平均收益模型
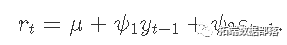
- mean如上述方程式中包括 。
- 按照norm 正态分布 。我们还将使用赤池信息准则(AIC)将拟合与学生t分布进行比较 。
- 使用将数据拟合到模型 ugarchfit。
ugarchspec(variance.model = list(model = "sGARCH",
garchOrder = c(1, 1)), mean.model = list(armaOrder = c(1,
0), include.mean = TRUE), distribution.model = "norm")
让我们看一下该模型中的条件分位数,也称为VaR,设置为99%。
## 首先是条件分位数
plot(fit, which = 2)
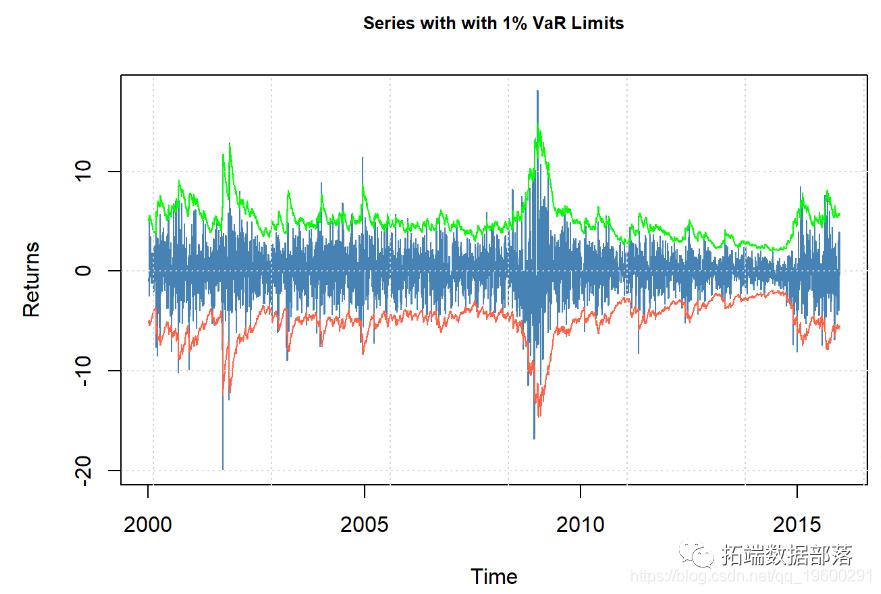
现在,让我们生成一个绘图面板。
## 数据acf-显示序列相关
plot(fit , which = 6)
## 数据的QQ图-显示标准化残基的峰度-不支持正态假设
## 标准化残差的acf
## 平方标准残差的acf

例子
让我们重做GARCH估计,现在使用Student t分布。
## 用学生t分布拟合AR(1)-GARCH(1,1)模型
AR.GARCH.spec <- ugarchspec(variance.model = list(model = "sGARCH",
garchOrder = c(1, 1)), mean.model = list(armaOrder = c(1,
0), include.mean = TRUE), distribution.model = "std")
结果
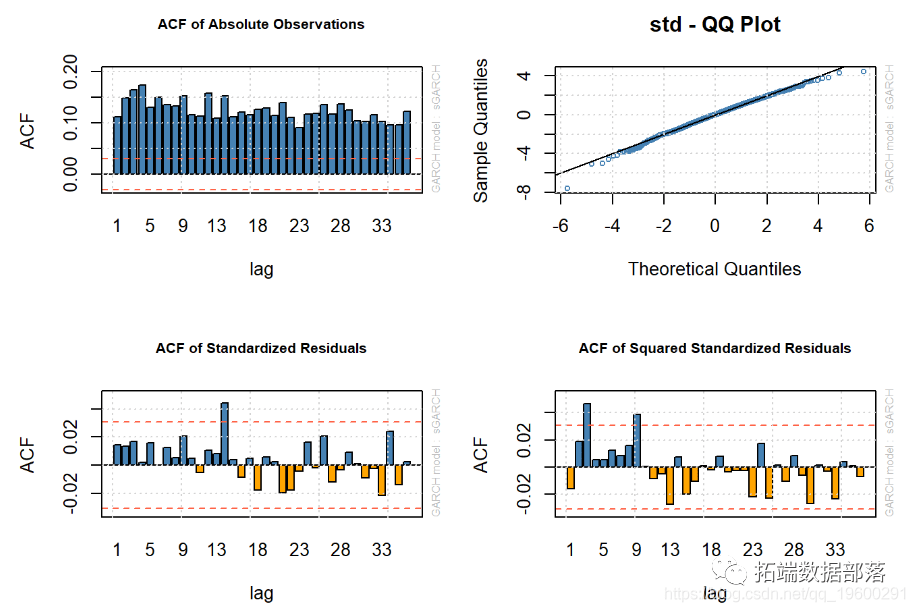
- 绝对观测值的ACF表明存在很大的波动性聚类。
- AR-ARCH估计具有有界的标准化残差(残差/标准误差),从而大大降低了这些误差。
- 看来t分布AR-GARCH解释了原油波动的大部分趋势。
用哪个模型?使用Akaike信息准则(AIC)测量模型中的信息。
使用正态分布模型的AIC = 4.2471。使用学生t分布模型的AIC = 4.2062。学生t分布模型更好。
这是我们可以从拟合模型中得出的一些常见结果:
## mu ar1 omega alpha1 beta1 shape
## 0.04018002 0.01727725 0.01087721 0.03816097 0.96074399 7.03778415
系数包括:
- mu 是原油的长期平均收益率。
- ar1 是一天后收益对今天收益的影响。
- omega 是长期方差。
- alpha1 滞后平方方差对今天的收益的影响。
- beta1 滞后平方残差对今天收益率的影响。
- shape 是学生t分布的自由度。
让我们来绘制随时间变化的波动性。
## mu ar1 omega alpha1 beta1 shape
## 0.04018002 0.01727725 0.01087721 0.03816097 0.96074399 7.03778415
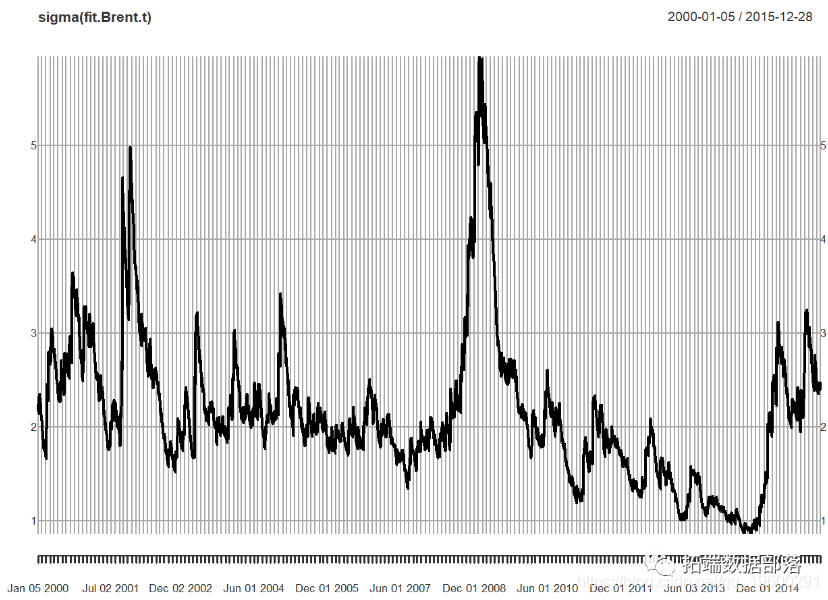
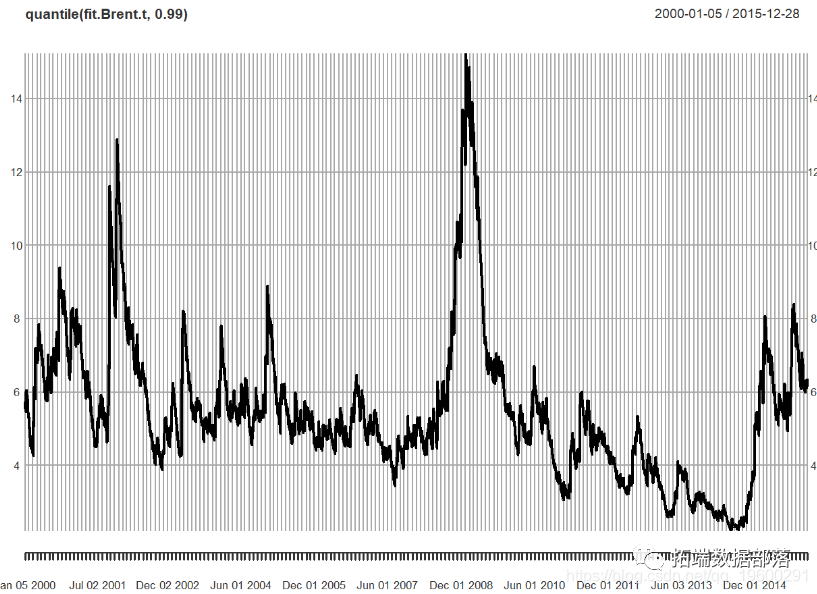
接下来,我们绘制并检验残差:
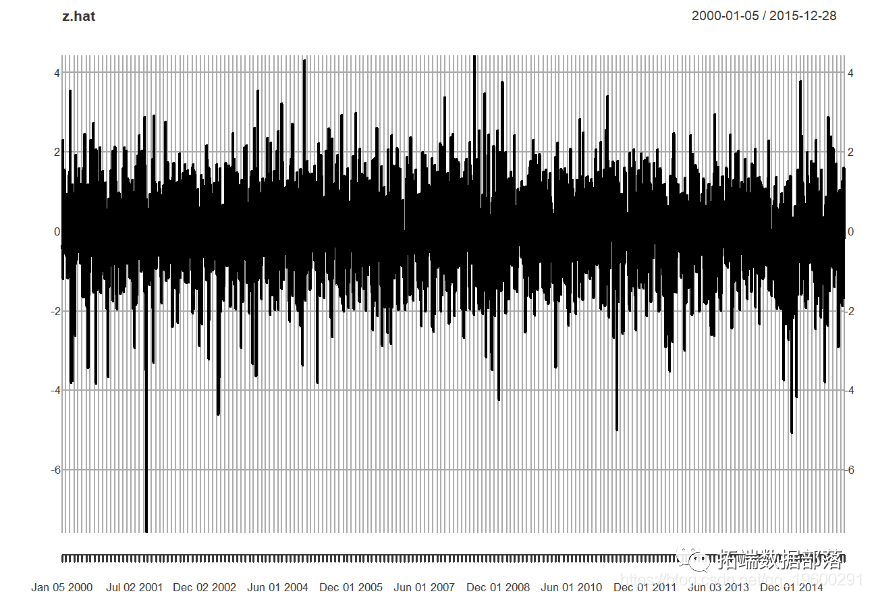
hist(z.hat)

mean(z.hat)
## [1] -0.0181139
var(z.hat)
## [,1]
## [1,] 1.000682
## [1] -0.3207327
## attr(,"method")
## [1] "moment"
kurtosis(z.hat)
## [1] 2.048561
## attr(,"method")
## [1] "excess"
##
## Shapiro-Wilk normality test
##
## data: as.numeric(z.hat)
## W = 0.98439, p-value < 2.2e-16
##
## Jarque-Bera Normality Test
##
## data: as.numeric(z.hat)
## JB = 780.73, p-value < 2.2e-16
## alternative hypothesis: greater
我们看到了什么?
- 左偏。
- 厚尾。
- 两种标准检验均表明拒绝该序列为正态分布的零假设。
模拟
- 使用fit 结果中的参数指定AR-GARCH。
- 生成2000条模拟路径。
GARCHspec
##
## *---------------------------------*
## * GARCH Model Spec *
## *---------------------------------*
##
## Conditional Variance Dynamics
## ------------------------------------
## GARCH Model : sGARCH(1,1)
## Variance Targeting : FALSE
##
## Conditional Mean Dynamics
## ------------------------------------
## Mean Model : ARFIMA(1,0,0)
## Include Mean : TRUE
## GARCH-in-Mean : FALSE
##
## Conditional Distribution
## ------------------------------------
## Distribution : std
## Includes Skew : FALSE
## Includes Shape : TRUE
## Includes Lambda : FALSE
## 生成长度为2000的两个路径
ugarchpath(GARCHspec, n.sim = 2000,
n.start = 50, m.sim = 2)
提取波动率
head(vol)
## [,1] [,2]
## T+1 2.950497 5.018346
## T+2 2.893878 4.927087
## T+3 2.848404 4.849797
## T+4 2.802098 4.819258
## T+5 2.880778 4.768916
## T+6 2.826746 4.675612


## 实际的模拟数据
X <- series$seriesSim
head(X)
## [,1] [,2]
## [1,] 0.1509418 1.4608335
## [2,] 1.2644849 -2.1509425
## [3,] -1.0397785 4.0248510
## [4,] 4.4369130 3.4214660
## [5,] -0.3076812 -0.1104726
## [6,] 0.4798977 2.7440751
示例
模拟的序列是否符合事实?
X1 <- X[, 1]
acf(X1)
acf(abs(X1))
qqnorm(X1)
qqline(X1, col = 2)
shapiro.test(X1)
这是结果

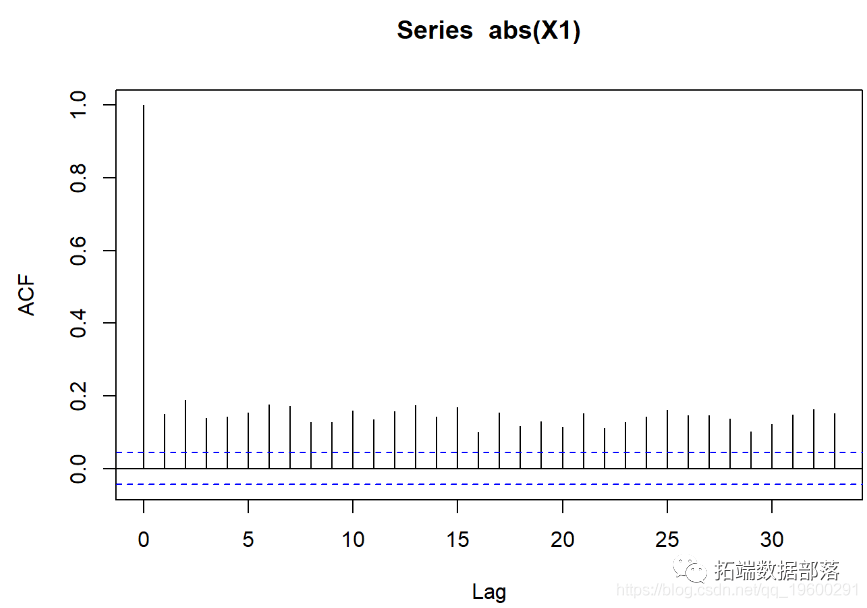
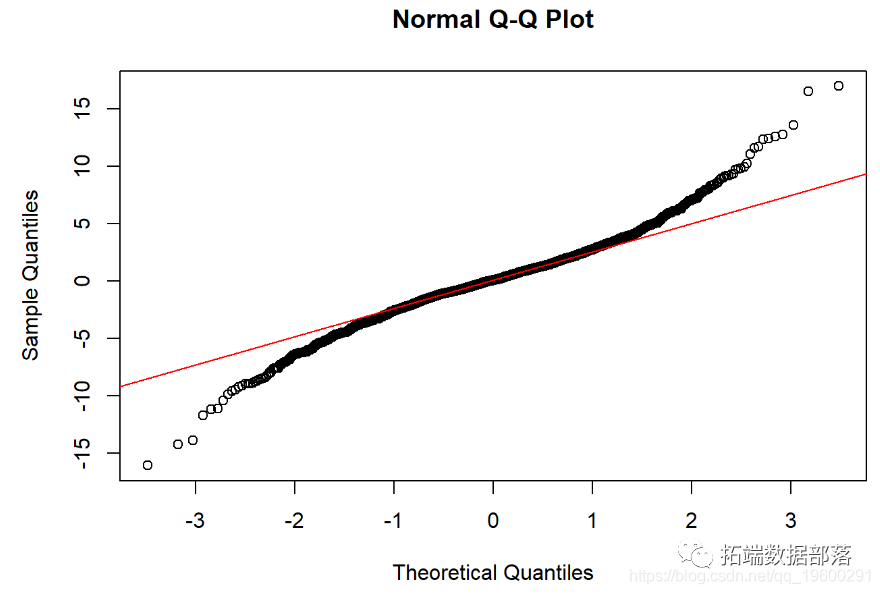
##
## Shapiro-Wilk normality test
##
## data: X1
## W = 0.97164, p-value < 2.2e-16
Shapiro-Wilk检验-零假设:正态分布。如果p值足够小,则拒绝原假设。-必须使用QQ图进行验证。
多元GARCH
从单变量GARCH到多元GARCH
- 动态条件相关。
- 具有随时间变化的波动性。
- 如何使资产收益之间的相关性也随时间变化。
为什么?-如果我们拥有投资组合(例如应收账款,可能会面临汇率和原油价格变动的情况),该怎么办?-我们需要了解这三个因素的联合波动性和依赖性,因为它们会影响应收账款的整体波动性。我们将使用这些条件方差来模拟管理货币和商品风险的工具的期权价格。
dcc.garch11.spec
##
## *------------------------------*
## * DCC GARCH Spec *
## *------------------------------*
## Model : DCC(1,1)
## Estimation : 2-step
## Distribution : mvt
## No. Parameters : 21
## No. Series : 3
现在进行拟合
现在让我们得到一些结果:
##
## *---------------------------------*
## * DCC GARCH Fit *
## *---------------------------------*
##
## Distribution : mvt
## Model : DCC(1,1)
## No. Parameters : 21
## [VAR GARCH DCC UncQ] : [0+15+3+3]
## No. Series : 3
## No. Obs. : 4057
## Log-Likelihood : -12820.82
## Av.Log-Likelihood : -3.16
##
## Optimal Parameters
## -----------------------------------
## Estimate Std. Error t value Pr(>|t|)
## [EUR.USD].mu 0.006996 0.007195 0.97238 0.330861
## [EUR.USD].omega 0.000540 0.000288 1.87540 0.060738
## [EUR.USD].alpha1 0.036643 0.001590 23.04978 0.000000
## [EUR.USD].beta1 0.962357 0.000397 2426.49736 0.000000
## [EUR.USD].shape 9.344066 1.192132 7.83811 0.000000
## [GBP.USD].mu 0.006424 0.006386 1.00594 0.314447
## [GBP.USD].omega 0.000873 0.000327 2.67334 0.007510
## [GBP.USD].alpha1 0.038292 0.002217 17.27004 0.000000
## [GBP.USD].beta1 0.958481 0.000555 1727.86868 0.000000
## [GBP.USD].shape 10.481272 1.534457 6.83061 0.000000
## [OIL.Brent].mu 0.040479 0.026696 1.51627 0.129450
## [OIL.Brent].omega 0.010779 0.004342 2.48228 0.013055
## [OIL.Brent].alpha1 0.037986 0.001941 19.57467 0.000000
## [OIL.Brent].beta1 0.960927 0.000454 2118.80489 0.000000
## [OIL.Brent].shape 7.040287 0.729837 9.64639 0.000000
## [Joint]dcca1 0.009915 0.002821 3.51469 0.000440
## [Joint]dccb1 0.987616 0.004386 225.15202 0.000000
## [Joint]mshape 9.732509 0.652707 14.91100 0.000000
##
## Information Criteria
## ---------------------
##
## Akaike 6.3307
## Bayes 6.3633
## Shibata 6.3306
## Hannan-Quinn 6.3423
##
##
## Elapsed time : 11.89964
- 联合条件协方差参数显着不同于零。
现在,使用来自拟合的所有信息,我们进行预测。我们用来模拟套期工具或投资组合VaR或ES,让我们先绘制随时间变化的sigma。
示例
鉴于条件波动性和相关性,请查看VaR和ES的三个风险因素。
这是一些结果。首先,计算,然后绘图。
## 1% 5% 50% 95% 99%
## -6.137269958 -3.677130793 -0.004439644 3.391312753 5.896992710
## 1% 5% 50% 95% 99%
## -1.3393119939 -0.8235076255 -0.0003271163 0.7659725631 1.2465945013
## 1% 5% 50% 95% 99%
## -1.520666396 -0.980794376 0.006889539 0.904772045 1.493169076
我们看到:
- 在分布的负数部分权重更大。
- 汇率大致相同。
- 如果您在客户和分销过程中使用布伦特原油,则可能会在约1%的时间内遭受600%以上的损失。
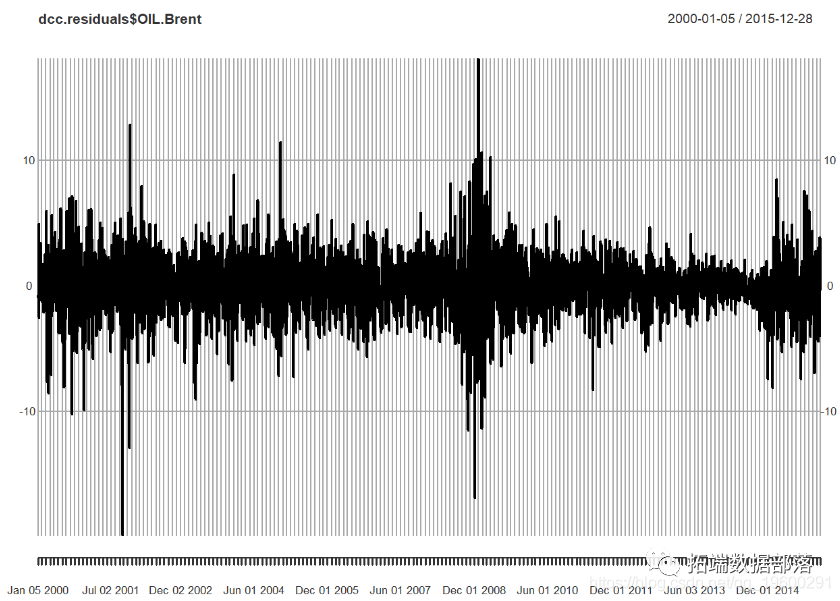
让我们使用新的波动率模型和分布进行调整,以拟合不对称和厚尾。
在这里,我们尝试使用一种新的GARCH模型:gjr代表Glosten,Jagannathan和Runkle(1993)他们提出的一个波动模型:
σ2t=ω+ασ2t-1+β1ε2t-1+β2ε2t-1It-1
拟合此模型。
##
## *---------------------------------*
## * GARCH Model Fit *
## *---------------------------------*
##
## Conditional Variance Dynamics
## -----------------------------------
## GARCH Model : gjrGARCH(1,1)
## Mean Model : ARFIMA(1,0,1)
## Distribution : nig
##
## Optimal Parameters
## ------------------------------------
## Estimate Std. Error t value Pr(>|t|)
## mu -0.040275 0.027883 -1.4445e+00 0.148608
## ar1 0.996072 0.001900 5.2430e+02 0.000000
## ma1 -0.989719 0.000005 -1.8786e+05 0.000000
## omega 0.006346 0.003427 1.8517e+00 0.064071
## alpha1 0.009670 0.003841 2.5178e+00 0.011808
## beta1 0.968206 0.001237 7.8286e+02 0.000000
## gamma1 0.042773 0.007183 5.9547e+00 0.000000
## skew -0.120184 0.032059 -3.7488e+00 0.000178
## shape 2.362890 0.351494 6.7224e+00 0.000000
##
## Robust Standard Errors:
## Estimate Std. Error t value Pr(>|t|)
## mu -0.040275 0.030871 -1.3046e+00 0.192023
## ar1 0.996072 0.002107 4.7283e+02 0.000000
## ma1 -0.989719 0.000005 -1.8363e+05 0.000000
## omega 0.006346 0.003388 1.8729e+00 0.061086
## alpha1 0.009670 0.004565 2.1184e+00 0.034143
## beta1 0.968206 0.000352 2.7485e+03 0.000000
## gamma1 0.042773 0.008503 5.0300e+00 0.000000
## skew -0.120184 0.033155 -3.6249e+00 0.000289
## shape 2.362890 0.405910 5.8212e+00 0.000000
##
## LogLikelihood : -8508.439
##
## Information Criteria
## ------------------------------------
##
## Akaike 4.1989
## Bayes 4.2129
## Shibata 4.1989
## Hannan-Quinn 4.2038
##
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 1.856 0.1730
## Lag[2*(p+q)+(p+q)-1][5] 2.196 0.9090
## Lag[4*(p+q)+(p+q)-1][9] 2.659 0.9354
## d.o.f=2
## H0 : No serial correlation
##
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 0.5109 0.474739
## Lag[2*(p+q)+(p+q)-1][5] 9.3918 0.013167
## Lag[4*(p+q)+(p+q)-1][9] 13.2753 0.009209
## d.o.f=2
##
## Weighted ARCH LM Tests
## ------------------------------------
## Statistic Shape Scale P-Value
## ARCH Lag[3] 10.26 0.500 2.000 0.001360
## ARCH Lag[5] 10.41 1.440 1.667 0.005216
## ARCH Lag[7] 11.06 2.315 1.543 0.010371
##
## Nyblom stability test
## ------------------------------------
## Joint Statistic: 2.5309
## Individual Statistics:
## mu 0.91051
## ar1 0.07050
## ma1 0.06321
## omega 0.70755
## alpha1 0.22126
## beta1 0.28137
## gamma1 0.17746
## skew 0.25115
## shape 0.16545
##
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic: 2.1 2.32 2.82
## Individual Statistic: 0.35 0.47 0.75
##
## Sign Bias Test
## ------------------------------------
## t-value prob sig
## Sign Bias 1.1836 0.23663
## Negative Sign Bias 0.7703 0.44119
## Positive Sign Bias 1.8249 0.06809 *
## Joint Effect 9.8802 0.01961 **
##
##
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
## group statistic p-value(g-1)
## 1 20 27.42 0.09520
## 2 30 46.32 0.02183
## 3 40 58.50 0.02311
## 4 50 70.37 0.02431
##
##
## Elapsed time : 6.630391
我们可以使用 tailplot() 函数解释结果。
## p quantile sfall
## [1,] 0.900 3.478474 5.110320
## [2,] 0.950 4.509217 6.293461
## [3,] 0.975 5.636221 7.587096
## [4,] 0.990 7.289163 9.484430
## [5,] 0.999 12.415553 15.368772
quantile 给出我们的风险价值(VaR)和期望损失(ES)
可以看到尾部图。
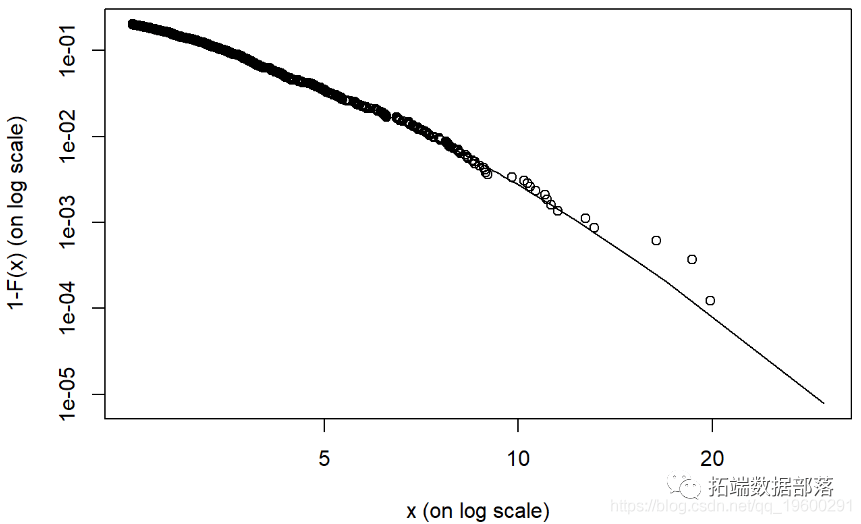
- 结果表明,使用AR-GARCH处理后,尾部更厚。
- 我们可以回到市场和风险部分,了解平均超额价值以及VaR和ES的置信区间。
- 对于应收帐款,缓解策略可能是通过再保险和_总收益互换_提供超额风险对冲。
- 对客户的信用风险分析至关重要:频繁更新客户将有助于及早发现某些解决方案的问题。

点击文末 “阅读原文”
获取全文完整资料。
本文选自 《R语言使用多元AR-GARCH模型衡量市场风险》 。
点击标题查阅往期内容
R语言GARCH模型对股市sp500收益率bootstrap、滚动估计预测VaR、拟合诊断和蒙特卡罗模拟可视化R语言单变量和多变量(多元)动态条件相关系数DCC-GARCH模型分析股票收益率金融时间序列数据波动率
R语言中的时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格
GARCH-DCC模型和DCC(MVT)建模估计
R语言预测期货波动率的实现:ARCH与HAR-RV与GARCH,ARFIMA模型比较
ARIMA、GARCH 和 VAR模型估计、预测ts 和 xts格式时间序列
Python/ target=_blank class=infotextkey>Python用GARCH、离散随机波动率模型DSV模拟估计股票收益时间序列与蒙特卡洛可视化
极值理论 EVT、POT超阈值、GARCH 模型分析股票指数VaR、条件CVaR:多元化投资组合预测风险测度分析
Garch波动率预测的区制转移交易策略
金融时间序列模型ARIMA 和GARCH 在股票市场预测应用
时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格
R语言风险价值:ARIMA,GARCH,Delta-normal法滚动估计VaR(Value at Risk)和回测分析股票数据
R语言GARCH建模常用软件包比较、拟合标准普尔SP 500指数波动率时间序列和预测可视化
Python金融时间序列模型ARIMA 和GARCH 在股票市场预测应用
MATLAB用GARCH模型对股票市场收益率时间序列波动的拟合与预测
R语言极值理论 EVT、POT超阈值、GARCH 模型分析股票指数VaR、条件CVaR:多元化投资组合预测风险测度分析
Python 用ARIMA、GARCH模型预测分析股票市场收益率时间序列
R语言中的时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格
R语言ARIMA-GARCH波动率模型预测股票市场苹果公司日收益率时间序列
Python使用GARCH,EGARCH,GJR-GARCH模型和蒙特卡洛模拟进行股价预测
R语言时间序列GARCH模型分析股市波动率
R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测
matlab实现MCMC的马尔可夫转换ARMA - GARCH模型估计
Python使用GARCH,EGARCH,GJR-GARCH模型和蒙特卡洛模拟进行股价预测
使用R语言对S&P500股票指数进行ARIMA + GARCH交易策略
R语言用多元ARMA,GARCH ,EWMA, ETS,随机波动率SV模型对金融时间序列数据建模
R语言股票市场指数:ARMA-GARCH模型和对数收益率数据探索性分析
R语言多元Copula GARCH 模型时间序列预测
R语言使用多元AR-GARCH模型衡量市场风险
R语言中的时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格
R语言用Garch模型和回归模型对股票价格分析
GARCH(1,1),MA以及历史模拟法的VaR比较
matlab估计arma garch 条件均值和方差模型