> Figure 1: The Monte Carlo Simulation method is used in many industries, from the stock market to finance, energy, banking, and other forecasting models. | Source: Pexels

Python 的蒙特卡罗仿真方法和应用程序的深入教程

作者：普拉蒂克·舒克拉，罗伯托·伊里翁多

什么是蒙特卡罗模拟？

蒙特卡罗方法是一种使用随机数和概率来解决复杂问题的技术。Monte Carlo 模拟（或概率模拟）是一种用于了解金融部门、项目管理、成本和其他预测机器学习模型中风险和不确定性影响的技术。

风险分析是我们几乎做出的每一个决策的一部分，因为我们不断面对生活中的不确定性、模糊性和多变性。此外，尽管我们拥有前所未有的信息获取机会，也无法准确预测未来。

蒙特卡罗模拟使我们能够查看决策的所有可能结果并评估风险影响，从而在不确定性下做出更好的决策。

在这篇文章中，我们将通过五个不同的例子来了解蒙特卡罗模拟方法。

资源：谷歌科拉布实施 |Github

应用：

• · 金融
• · 能源
• · 制造
• · 工程
• · 研发
• · 保险
• · 石油和天然气
• · 运输
• · 环境
• · 其他

例子：

· 硬币翻转示例

· 使用圆和方形估算 PI

· 蒙蒂大厅问题

· 布冯投针的问题

· 为什么庄家总是赢

1. 硬币翻转示例：

公平硬币的正面概率为1/2。然而，有什么办法我们可以用实验来证明吗？在此示例中，我们将使用 Monte-Carlo 方法以 5000 次迭代方式模拟硬币翻转，以找出为什么正面或反面的概率始终为 1/2。如果我们重复这个硬币翻转很多，很多次，那么我们可以达到更高的精度，一个确切的答案，我们的概率值。

> Figure 2: Heads and tails, mathematical representation.

 

翻转硬币时：

> Figure 3: Formula for heads and tails coin example.

 

接下来，我们将用蒙特卡罗方法以实验方式证明这个公式。

Python 实现：

· 导入所需的库：

> Figure 4: Import the required libraries for our coin flipping example.

 

1. 硬币翻转功能：

> Figure 5: A simple function randomizing the results between 0 and 1, 0 for heads, and 1 for tails.

 

2. 检查函数的输出：

> Figure 6: Running the function of coin_flip()

 

3. 主函数：

> Figure 7: Calculating the probability and Appending the probability values to the results.

 

4. 调用主函数：

> Figure 8: Calling the Monte Carlo main function, along with plotting final values.

 

如图 8 所示，我们显示 5000 次迭代后，获得反面的概率为 0.502。因此，我们如何使用蒙特卡罗模拟来实验地找到概率。

2. 使用圆和正方形估算 PI：

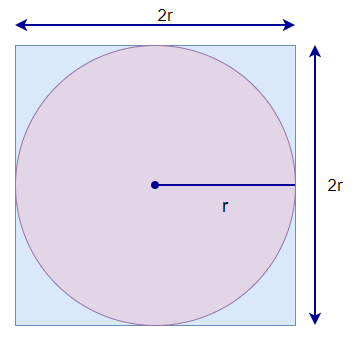
> Figure 9: Simple area of a circle and of a square.

 

> Figure 10: Calculation of the area of a circle and square respectively.

 

为了估计 PI 的值，我们需要正方形的面积和圆的面积。要查找这些区域，我们将随机在曲面上放置点，并计算落在圆内的点和位于正方形内的点。这将给我们估计他们的面积。因此，我们将使用点计数作为区域，而不是使用实际区域。

在下面的代码中，我们使用 Python 的海龟模块来查看点的随机放置。

Python 实现：

1.导入所需的库：

> Figure 10: Importing required libraries for our π example.

 

2.可视化作图

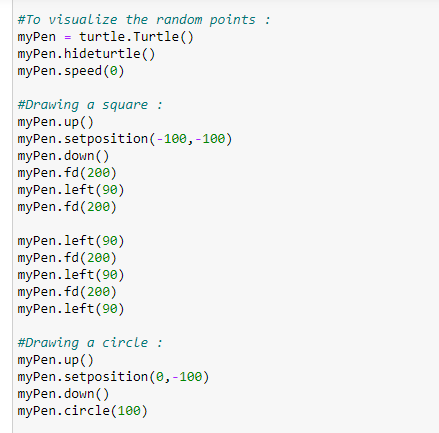
> Figure 11: Drawing the figures.

 

3. 初始化一些必需的数据：

> Figure 12: Initializing data values.

 

4. 主函数：

> Figure 13: Implementing the main function.

 

5. 绘制数据：

> Figure 14: Plotting the data values.

 

6. 输出：

> Figure 15: π approximations using the Monte Carlo methodology.

 

> Figure 16: Data visualization of the values.

 

> Figure 17: Data visualization of the values.

 

如图 17 所示，我们可以看到，在 5000 次迭代之后，我们可以获得 PI 的近似值。此外，请注意，随着迭代次数的增加，估计误差也呈指数级下降。

 

通过 Python 中的代码示例，查看初学者的机器学习算法概述。

3. 蒙蒂大厅问题：

假设你在游戏表演，你可以选择选择三扇门之一：一扇门后面是一辆车;在其他门后面，山羊。你选一扇门，让我们说门1，主人，谁知道门后面是什么，打开另一扇门，说门3，它有一只山羊。然后主人问你：你是要坚持自己的选择还是选择另一扇门？[1]

切换您选择的门对您有利吗？

根据概率，事实证明，切换门对我们有利。让我们了解如何：

最初，对于所有三个门，获得汽车的概率 （P） 是相同的 （P = 1/3）。

 

> Figure 18: A simulation of the three gates for our game show, showcasing each of the possible outcomes.

现在假设参赛者选择门 1。接下来，主人打开第三扇门，它有一只山羊。接下来，主持人问参赛者是否想换门？

我们将了解为什么切换门更有利：

> Figure 19: A figurative outcome for the door gameshow.

 

在图 19 中，我们可以看到主机打开车门 3 后，最后两扇门有车的概率增加至 2/3。现在我们知道第三扇门有一只山羊，第二扇门有车的概率增加到2/3。因此，切换门更有利。

 

Python 实现：

1.导入所需的库：

> Figure 20: Importing required libraries for our game show example.

 

2. 初始化某些数据：

> Figure 21: Initializing the doors and empty lists to store the probability values.

 

3. 主函数：

> Figure 22: Implementing the main function with a Monte Carlo Simulation method.

 

4. 调用主函数：

> Figure 23: Calling the main function of our game show example, and interesting 1000 times.

 

5. 输出：

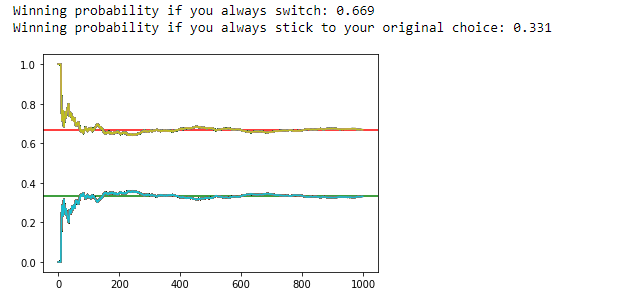
> Figure 24: Approximate winning probabilities to sticking with your choice or switching doors.

在图 24 中，我们显示 1000 次迭代后，如果我们切换门，获胜概率为 0.669。因此，我们相信，在此示例中切换门对我们的优势是管用。

4. 布冯投针的问题：

1777年[2][3]，法国贵族乔治-路易斯·勒克莱克（Comte de Buffon）发布了以下问题。

假设我们把一根短针掉在有横条的纸上——针头躺在穿过其中一条线的位置的概率是多少？

概率取决于被统治纸张的线之间的距离 （d），它取决于我们掉落的针的长度 （l），或者更确切地说，它取决于比率 l/d。对于此示例，我们可以将针头解释为 l ≤ d。简而言之，我们的目的是针不能同时穿过两条不同的线。令人惊讶的是，布冯的针头问题的答案涉及PI。

在这里，我们将使用布冯的针头问题的解决方案，以实验方式使用蒙特卡罗方法估计PI的价值。然而，在进入之前，我们将展示解决方案是如何派生的，使其更有趣。

定理：

如果将长度为 l 的短针掉到以相同距离 d ≥ l 的相等空间线裁定的纸张上，则针位于穿过其中一条线的位置的概率为：

> Figure 25: Buffon's needle problem theorem.

 

可视化投针问题

> Figure 26: Visualizing Buffon's needle problem.

 

接下来，我们需要计算穿过任何垂直线的针数。对于要与其中一条线相交的指针，对于 theta 的特定值，以下是针与垂直线相交的最大值和最小可能值。

1.最大可能值：

> Figure 27: Maximum possible value.

 

2. 最小可能值：

> Figure 28: Minimum possible value.

 

因此，对于 theta 的特定值，针位于垂直线上的概率为：

> Figure 29: Probability for a needle to lie on a vertical line formula.

 

上述概率公式仅限于一个值;在我们的实验中，theta 的值范围从0到pi/2。接下来，我们将通过集成它来查找实际概率，以结合所有 to 的值。

> Figure 30: Probability formula by integrating all possible values for theta.

 

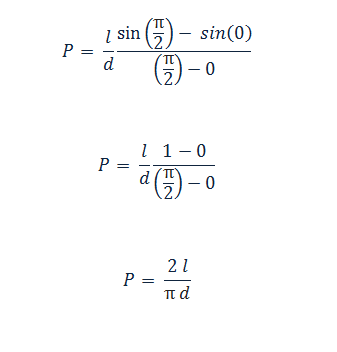
> Figure 31: PI estimation.

 

使用布冯投针问题估算 PI：

接下来，我们将使用上述公式来实验找出PI的值。

> Figure 32: Finding the value of PI.

 

现在，请注意，我们有 l 和 d 的值。我们的目标是首先找到 P 的值，以便获得 PI 的值。要找到概率P，我们必须需要打针和总针的计数。由于我们已经有总针的计数，我们现在唯一需要的东西是打针的计数。

下面是我们如何计算命中针数的可视化表示。

> Figure 33: Visual representation to calculate the count of needles.

 

Python 实现：

1.导入所需的库：

> Figure 34: Importing the required libraries for our problem.

 

3. 主函数：

> Figure 35: Implementing the Monte Carlo Simulation method to our Buffon problem.

 

3. 调用主函数：

> Figure 36: Calling the Monte Carlo Method's main function to our Buffon's problem.

 

4. 输出：

> Figure 37: Data visualization of 100 iterations using the Monte Carlo Method.

> Source: Pexels

 

5. 为什么庄家总是赢？

赌场如何赚钱？诀窍很简单——"你玩得越多，他们赚得越多。让我们看一下这如何与一个简单的蒙特卡罗模拟示例。

考虑一个假想的游戏，玩家必须从一袋筹码中选择筹码。

规则：

· 袋子里有1~100个不等的筹码。

· 用户可以投注偶数或奇数筹码。

· 在这个游戏中，10 和 11 是特殊数字。如果我们在偶数上下注，则 10 将计为奇数，如果我们下注赔率，则 11 将计为偶数。

· 如果我们赌上甚至数字， 我们得到 10， 然后我们输了。

· 如果我们赌奇数， 我们得到 11， 然后我们输了。

如果我们押注赔率，我们获胜的概率是49/100。庄家获胜的概率为 51/100。因此，对于奇怪的赌注，庄家 边缘是 = 51/100×49/100 = 200/10000 = 0.02 = 2%

如果我们押注均数，用户获胜的概率为 49/100。庄家获胜的概率为 51/100。因此，对于一个奇怪的赌注，庄家的边缘是 = 51/100×49/100 = 200/10000 = 0.02 = 2%

总之，每1美元的赌注，0.02美元去的会被庄家赢走。相比之下，轮盘赌的最低庄家边缘为2.5%。因此，我们确信，你将有更好的机会赢得我们想象中的游戏轮盘赌。

Python 实现：

1.导入所需的库：

> Figure 38: Importing the required libraries for our casino problem.

 

2.初始化

> Figure 39: Placing bets for odds and even numbers.

 

3. 主函数：

> Figure 40: Applying the Monte Carlo Methodology to our casino problem.

 

4. 最终输出：

> Figure 41: Calculating and displaying the final values.

 

5. 运行 1000 次迭代：

> Figure 42: Running our function 1000 times.

 

6. 投注数量 = 5：

> Figure 43: Data visualization of results when the number of bets equals five.

 

7. 投注数量 = 10：

> Figure 44: Data visualization of results when the number of bets equals ten.

 

8. 投注数量 = 1000：

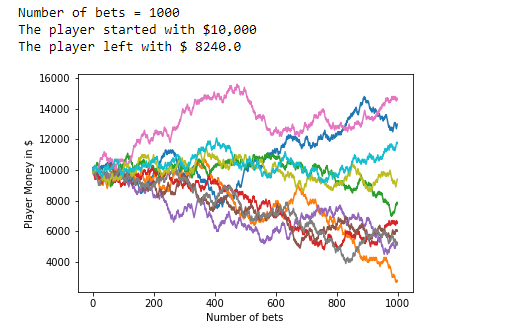
> Figure 45: Data visualization of results when the number of bets equals 1000.

 

9. 投注数量 = 5000：

> Figure 46: Data visualization of results when the number of bets equals 5000.

 

10. 投注数量 = 10000：

> Figure 47: Data visualization of results when the number of bets equals 10000.

从上面的实验中，我们可以看到，如果玩家在这些游戏上下注较少，他们有更好的盈利机会。在某些情况下，我们得到负数，这意味着玩家失去了所有的钱和累积的债务，而不是盈利。

请记住，这些百分比是我们的模拟游戏，他们可以修改。

结论：

与任何预测模型一样，仿真将只像我们估计得一样好。重要的是要记住，蒙特卡罗模拟只代表概率，而不是确定性。然而，蒙特卡罗模拟可以是一个有价值的工具，当预测一个未知的未来。

详细介绍我们的神经网络教程，详细介绍 Python 代码和数学

免责声明：本文所表达的观点是作者的观点，并不代表卡内基梅隆大学的观点。这些著作并不打算成为最终产品，而是反映当前思维，同时成为讨论和改进的催化剂。

引用：

[1] 概率问题报价， 21 电影， https://www.imdb.com/title/tt0478087/characters/nm0000228#quotes

[2] 乔治-路易斯·勒克莱克，布冯伯爵，维基百科，https://en.wikipedia.org/wiki/Georges-Louis_Leclerc,_Comte_de_Buffon

[3] 布冯投针问题，维基百科，https://en.wikipedia.org/wiki/Buffon%27s_needle_problem

 

(本文翻译自Towards AI Team的文章《Monte Carlo Simulation An In-depth Tutorial with Python》，参考：https://medium.com/towards-artificial-intelligence/monte-carlo-simulation-an-in-depth-tutorial-with-python-bcf6eb7856c8)